Constitutive modeling¶
Kinematics of strain¶
${}$
"2D geometric strain" by Sanpaz. Licensed under Public Domain via Wikimedia Commons.
Strain tensor¶
${}$
$$ \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{bmatrix} $$
$$\varepsilon_{ij} = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) \quad \mbox{for} \quad i=1,2,3 \quad j=1,2,3$$
Volumetric strain¶
$$ \varepsilon_{vol} = \mbox{tr}(\boldsymbol{\varepsilon}) = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} $$Typical Young's modulus values¶
${}$
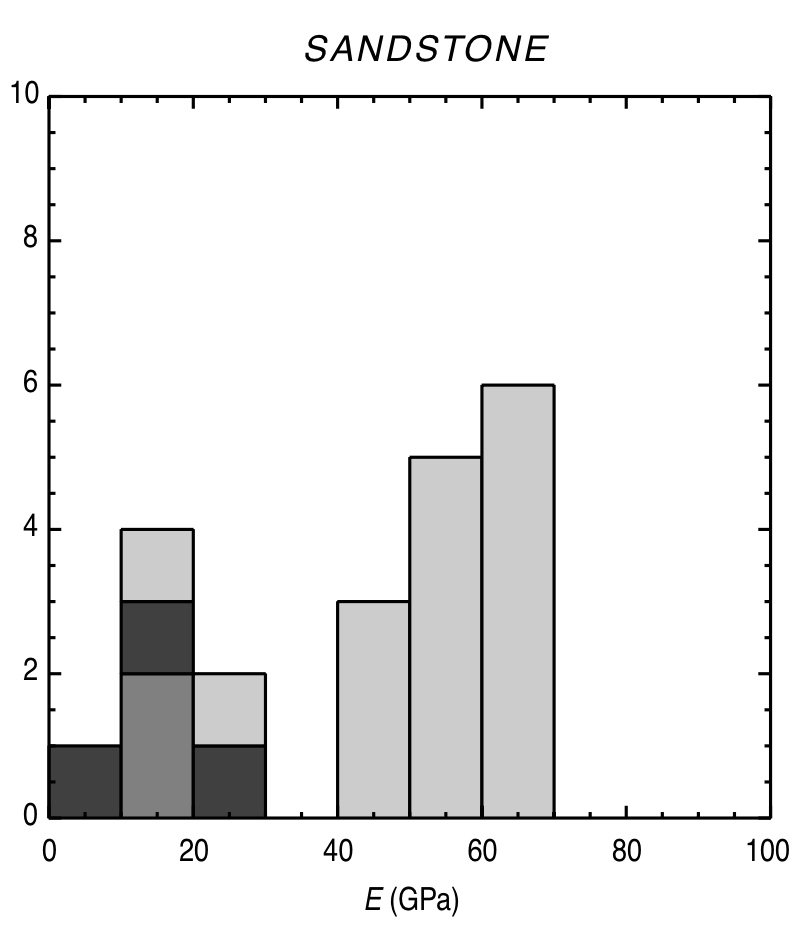 |
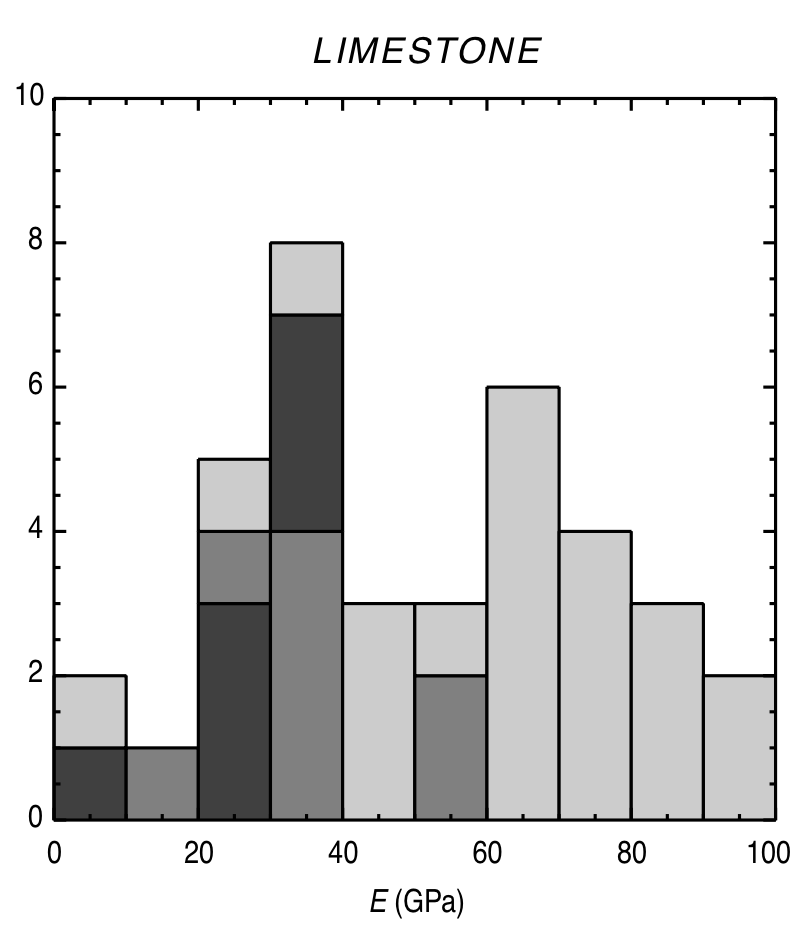 |
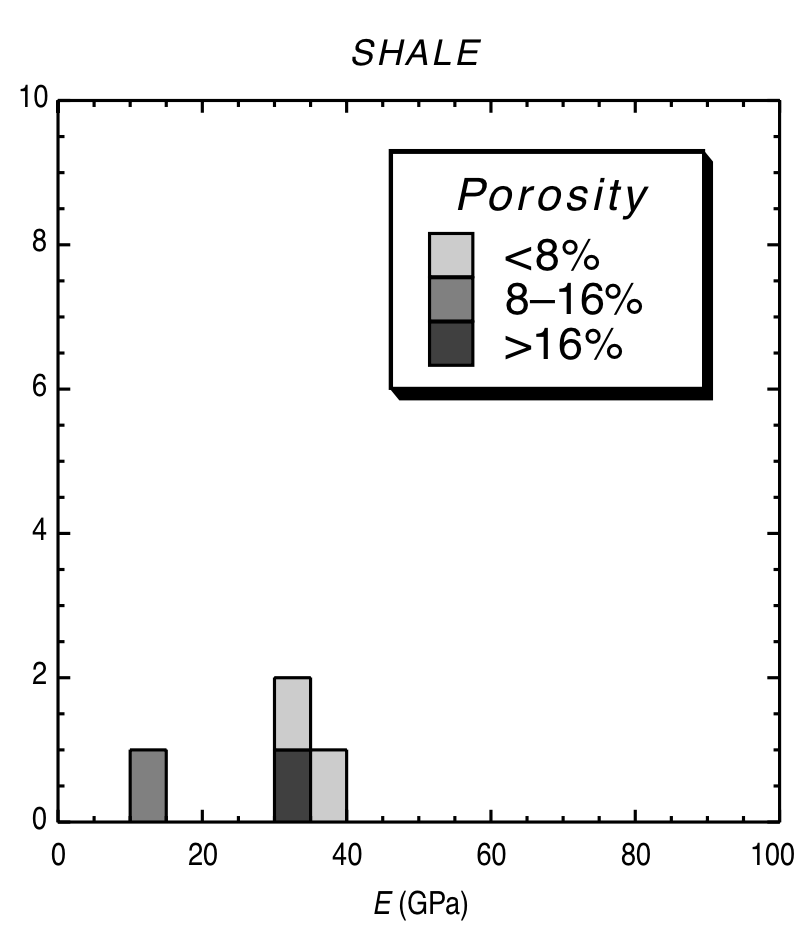 |
© Lama, R. D., and V. S. Vutukuri. HANDBOOK ON MECHANICAL PROPERTIES OF ROCKS-TESTING TECHNIQUES AND RESULTS. VOLUME 2. Monograph. 1978.)
Typical Poissons' modulus values¶
${}$
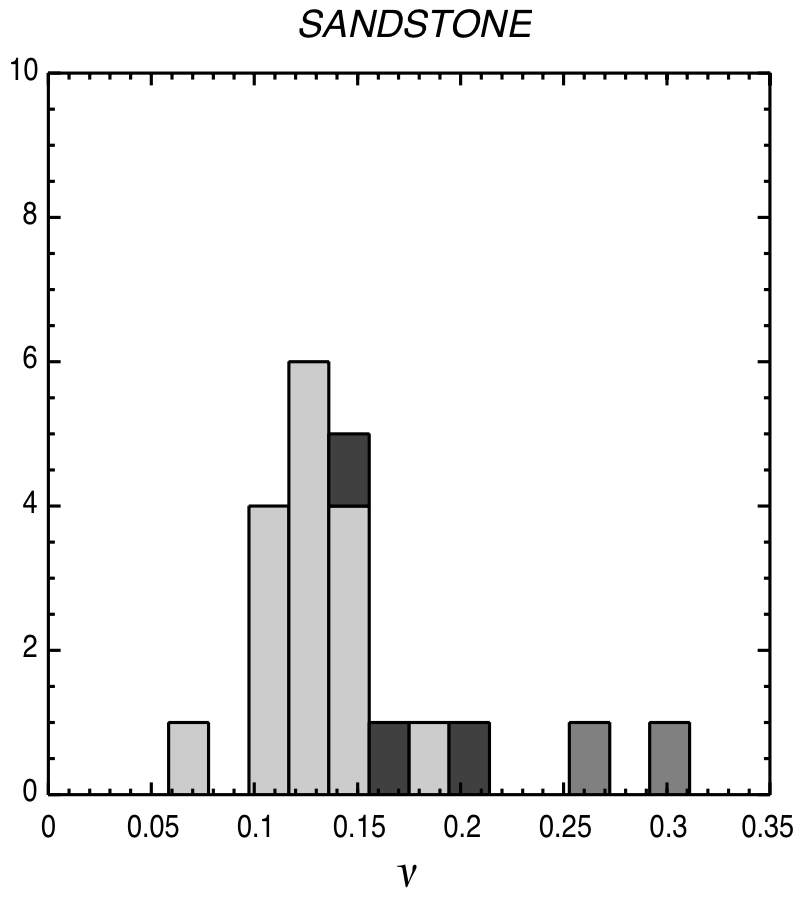 |
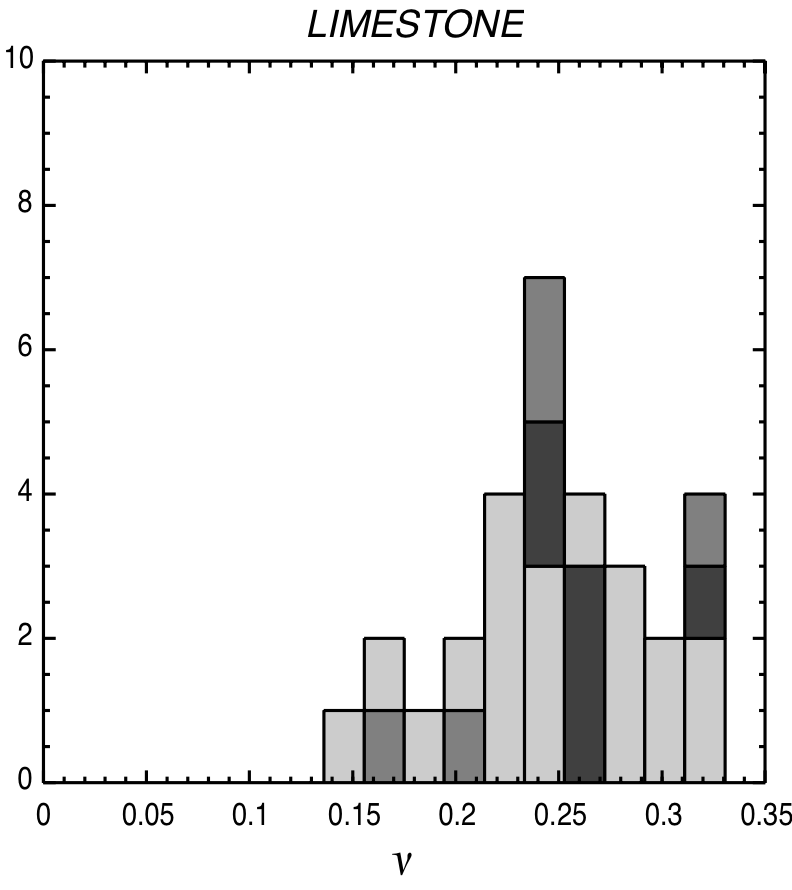 |
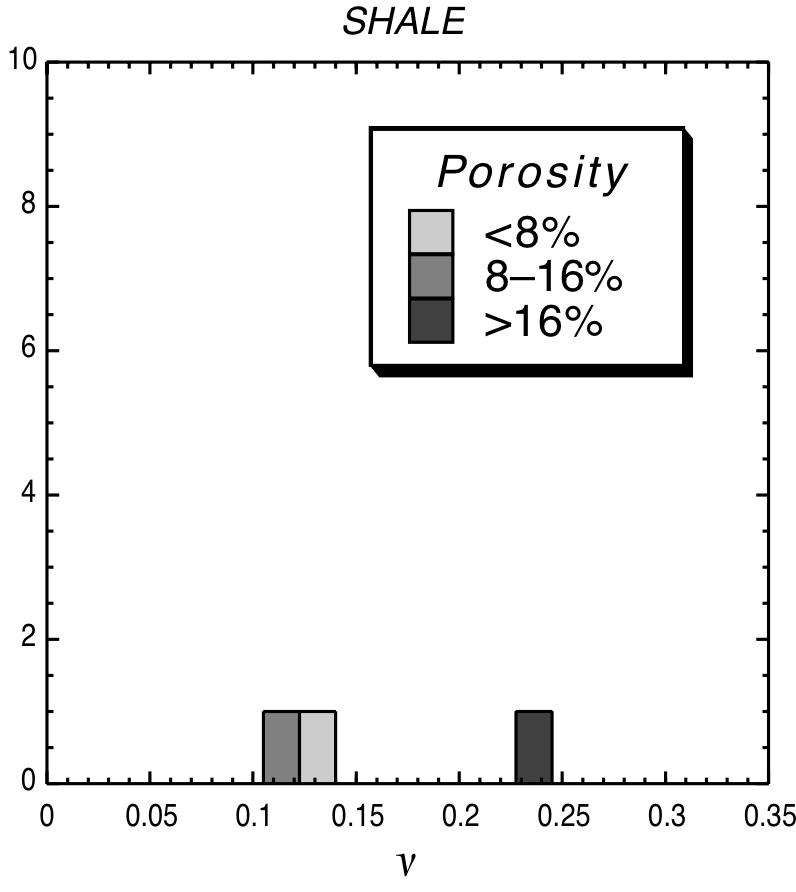 |
© Lama, R. D., and V. S. Vutukuri. HANDBOOK ON MECHANICAL PROPERTIES OF ROCKS-TESTING TECHNIQUES AND RESULTS. VOLUME 2. Monograph. 1978.)
Generalized Hooke's law¶
${}$
$$\vec{\sigma} = \boldsymbol{C} \, \vec{\varepsilon}$$For isotropic materials¶
\begin{equation} \small \left\lbrace\begin{matrix} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{12} \\ \sigma_{13} \\ \sigma_{23} \end{matrix}\right\rbrace = \frac{E}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 - \nu & \nu & \nu & 0 & 0 & 0 \\ \nu & 1 - \nu & \nu & 0 & 0 & 0 \\ \nu & \nu & 1 - \nu & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) \end{bmatrix} \left\lbrace\begin{matrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{33} \\ 2\varepsilon_{12} \\ 2\varepsilon_{13} \\ 2\varepsilon_{23} \end{matrix}\right\rbrace \end{equation}
$$\mathbf{S} = K \varepsilon_{vol} \mathbf{I} + 2 G \left(\boldsymbol{\varepsilon} - \frac{1}{3} \varepsilon_{vol}\mathbf{I}\right)$$$$G = \frac{E}{2(1+\nu)} \Rightarrow \mbox{shear modulus}$$
$$\mathbf{S} = \lambda \varepsilon_{vol} \mathbf{I} + 2 G \boldsymbol{\varepsilon} $$$$\lambda = K - \frac{2}{3} G \Rightarrow \text{Lamé's constant}$$
Relationships between constants¶
| $K=\,$ | $E=\,$ | $\lambda=\,$ | $G=\,$ | $\nu=\,$ | $M=\,$ | |
| $(K,\,E)$ | $K$ | $E$ | $\tfrac{3K(3K-E)}{9K-E}$ | $\tfrac{3KE}{9K-E}$ | $\tfrac{3K-E}{6K}$ | $\tfrac{3K(3K+E)}{9K-E}$ |
| $(K,\,\lambda)$ | $K$ | $\tfrac{9K(K-\lambda)}{3K-\lambda}$ | $\lambda$ | $\tfrac{3(K-\lambda)}{2}$ | $\tfrac{\lambda}{3K-\lambda}$ | $3K-2\lambda\,$ |
| $(K,\,G)$ | $K$ | $\tfrac{9KG}{3K+G}$ | $K-\tfrac{2G}{3}$ | $G$ | $\tfrac{3K-2G}{2(3K+G)}$ | $K+\tfrac{4G}{3}$ |
| $(K,\,\nu)$ | $K$ | $3K(1-2\nu)\,$ | $\tfrac{3K\nu}{1+\nu}$ | $\tfrac{3K(1-2\nu)}{2(1+\nu)}$ | $\nu$ | $\tfrac{3K(1-\nu)}{1+\nu}$ |
| $(K,\,M)$ | $K$ | $\tfrac{9K(M-K)}{3K+M}$ | $\tfrac{3K-M}{2}$ | $\tfrac{3(M-K)}{4}$ | $\tfrac{3K-M}{3K+M}$ | $M$ |
| $(E,\,\lambda)$ | $\tfrac{E + 3\lambda + R}{6}$ | $E$ | $\lambda$ | $\tfrac{E-3\lambda+R}{4}$ | $\tfrac{2\lambda}{E+\lambda+R}$ | $\tfrac{E-\lambda+R}{2}$ |
| $(E,\,G)$ | $\tfrac{EG}{3(3G-E)}$ | $E$ | $\tfrac{G(E-2G)}{3G-E}$ | $G$ | $\tfrac{E}{2G}-1$ | $\tfrac{G(4G-E)}{3G-E}$ |
| $(E,\,\nu)$ | $\tfrac{E}{3(1-2\nu)}$ | $E$ | $\tfrac{E\nu}{(1+\nu)(1-2\nu)}$ | $\tfrac{E}{2(1+\nu)}$ | $\nu$ | $\tfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}$ |
| $(E,\,M)$ | $\tfrac{3M-E+S}{6}$ | $E$ | $\tfrac{M-E+S}{4}$ | $\tfrac{3M+E-S}{8}$ | $\tfrac{E-M+S}{4M}$ | $M$ |
| $(\lambda,\,G)$ | $\lambda+ \tfrac{2G}{3}$ | $\tfrac{G(3\lambda + 2G)}{\lambda + G}$ | $\lambda$ | $G$ | $\tfrac{\lambda}{2(\lambda + G)}$ | $\lambda+2G\,$ |
| $(\lambda,\,\nu)$ | $\tfrac{\lambda(1+\nu)}{3\nu}$ | $\tfrac{\lambda(1+\nu)(1-2\nu)}{\nu}$ | $\lambda$ | $\tfrac{\lambda(1-2\nu)}{2\nu}$ | $\nu$ | $\tfrac{\lambda(1-\nu)}{\nu}$ |
| $(\lambda,\,M)$ | $\tfrac{M + 2\lambda}{3}$ | $\tfrac{(M-\lambda)(M+2\lambda)}{M+\lambda}$ | $\lambda$ | $\tfrac{M-\lambda}{2}$ | $\tfrac{\lambda}{M+\lambda}$ | $M$ |
| $(G,\,\nu)$ | $\tfrac{2G(1+\nu)}{3(1-2\nu)}$ | $2G(1+\nu)\,$ | $\tfrac{2 G \nu}{1-2\nu}$ | $G$ | $\nu$ | $\tfrac{2G(1-\nu)}{1-2\nu}$ |
| $(G,\,M)$ | $M - \tfrac{4G}{3}$ | $\tfrac{G(3M-4G)}{M-G}$ | $M - 2G\,$ | $G$ | $\tfrac{M - 2G}{2M - 2G}$ | $M$ |
| $(\nu,\,M)$ | $\tfrac{M(1+\nu)}{3(1-\nu)}$ | $\tfrac{M(1+\nu)(1-2\nu)}{1-\nu}$ | $\tfrac{M \nu}{1-\nu}$ | $\tfrac{M(1-2\nu)}{2(1-\nu)}$ | $\nu$ | $M$ |
