Rock failure

Types of tests on rocks

Hydrostatic compression

$$S_0 = S_1 = S_2 = S_3$$

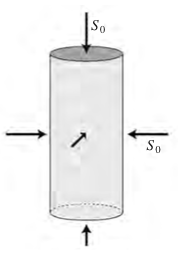
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.1, pp. 86)

Uniaxial compression

$$S_0 \ne 0 \quad S_2 = S_3 = 0$$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.1, pp. 86)

Triaxial compression

$$S_1 > S_2 = S_3$$

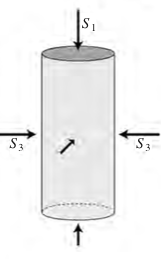
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.1, pp. 86)

Triaxial extension

$$S_1 = S_2 > S_3$$

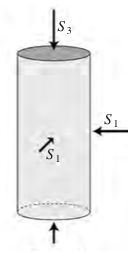
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.1, pp. 86)

True triaxial

$$S_1 \ne S_2 \ne S_3$$

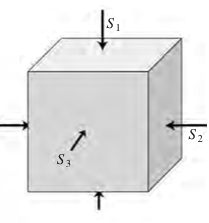
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.1, pp. 86)

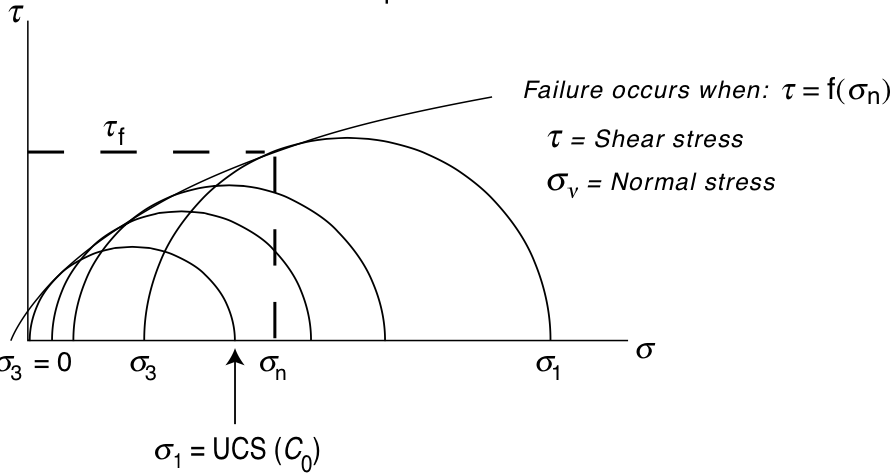
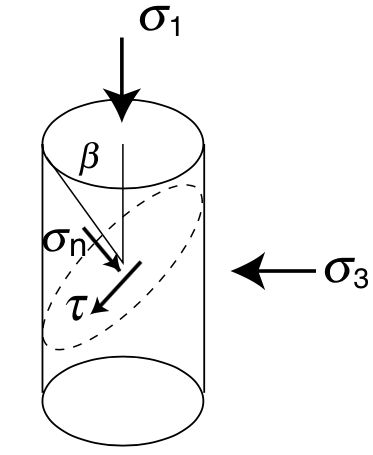
Mohr's circles

$$\tau_f = \dfrac{1}{2}(\sigma_1 - \sigma_3) \sin(2\beta)$$$$\sigma_n = \dfrac{1}{2}(\sigma + \sigma_3) + \dfrac{1}{2}(\sigma_1 -\sigma_3) \cos(2 \beta)$$

Mohr Envelope

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.2b, pp. 88)

Linearized Mohr Envelope

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.2a,c pp. 88)

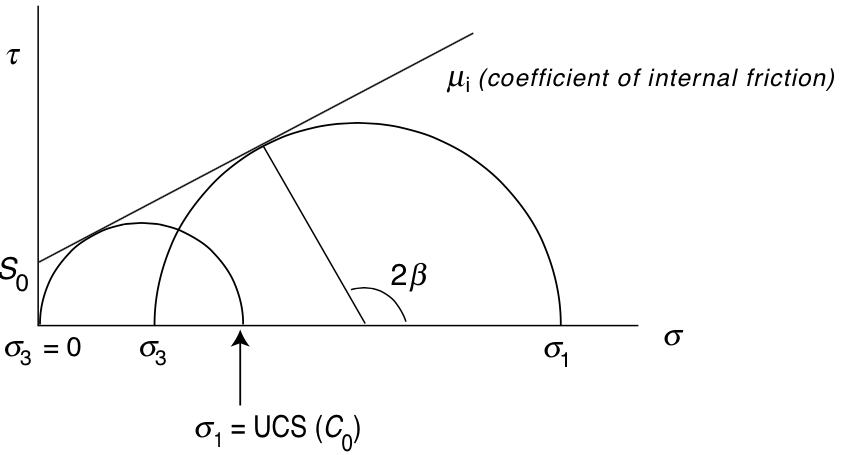
Mohr-Coulomb failure

${}$

$$ \tau = S_0 + \sigma_n \mu_i $$

$$ C_0 = 2 S_0\left( \sqrt{\mu_i^2 + 1} + \mu_i \right) $$

Triaxial tests on sandstone

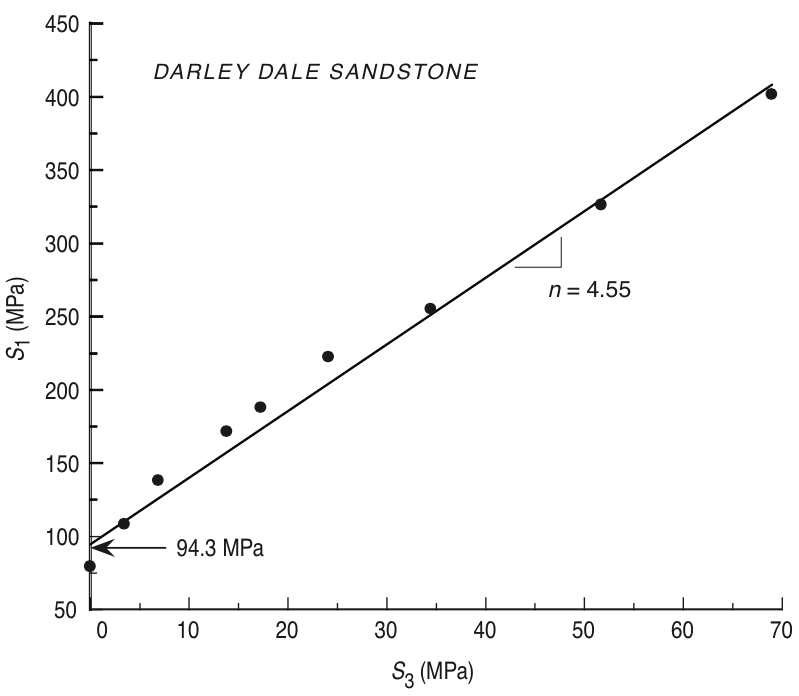$\mu_i = \dfrac{n-1}{2\sqrt{n}}$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.3a pp. 90)

Mohr Envelope for Sandstone

${}$

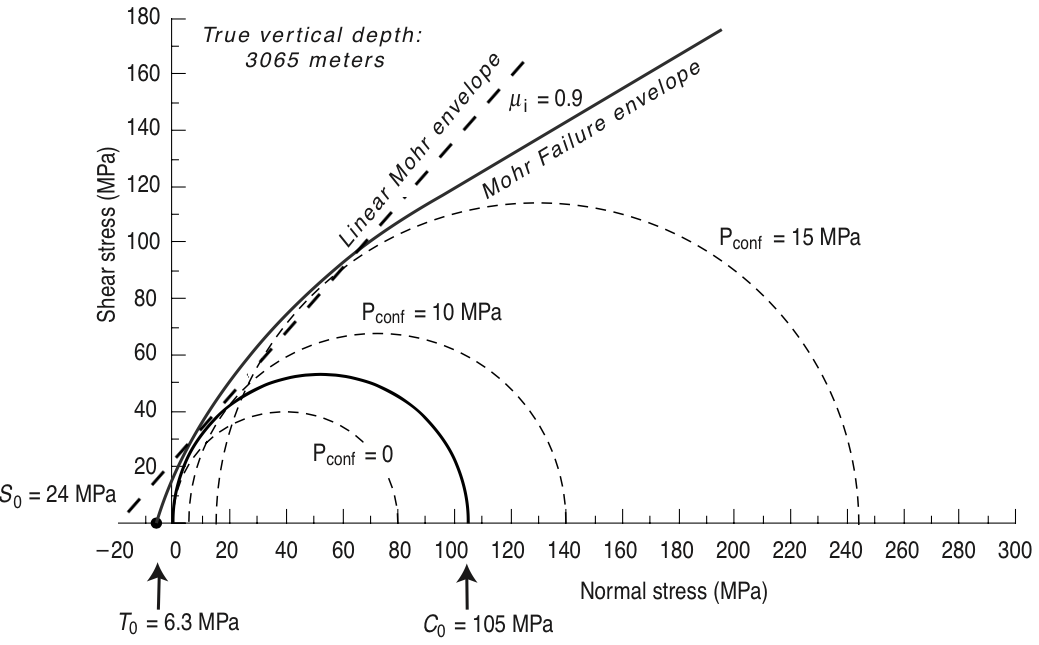
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.3a, pp. 88)

Cohesion and internal friction data

${}$

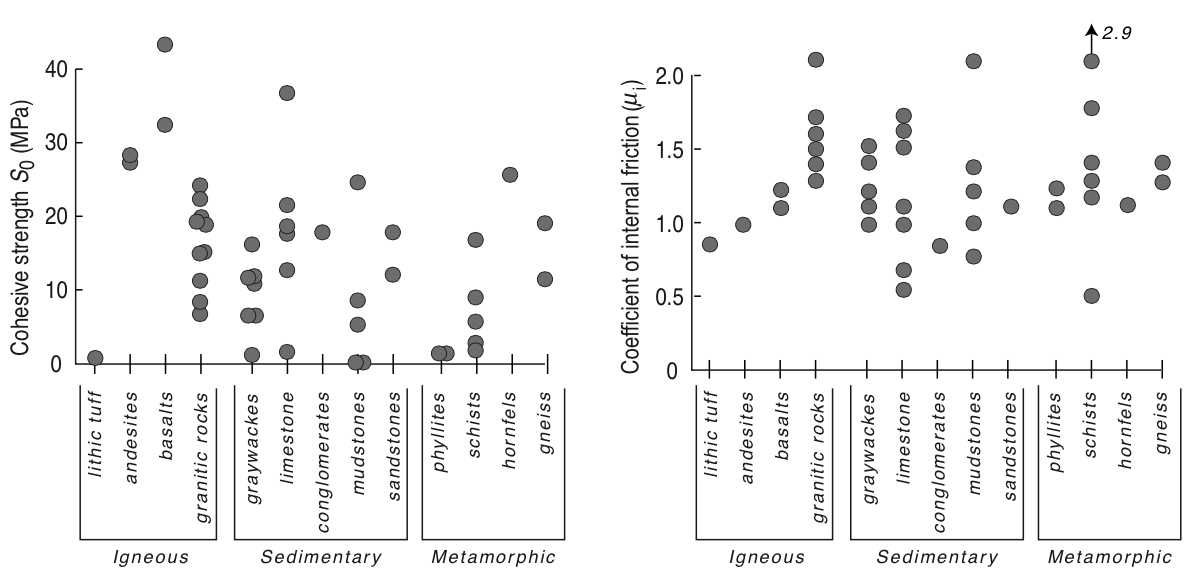
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.4, pp. 91)

Cohesion and internal friction data

${}$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.5, pp. 92)

Yield surface

Mohr Coulomb Yield Surface 3Da. Licensed under CC BY-SA 3.0 via Wikipedia

$\pi$-plane

Mohr Coulomb Yield Surface 3Db. Licensed under CC BY-SA 3.0 via Wikipedia

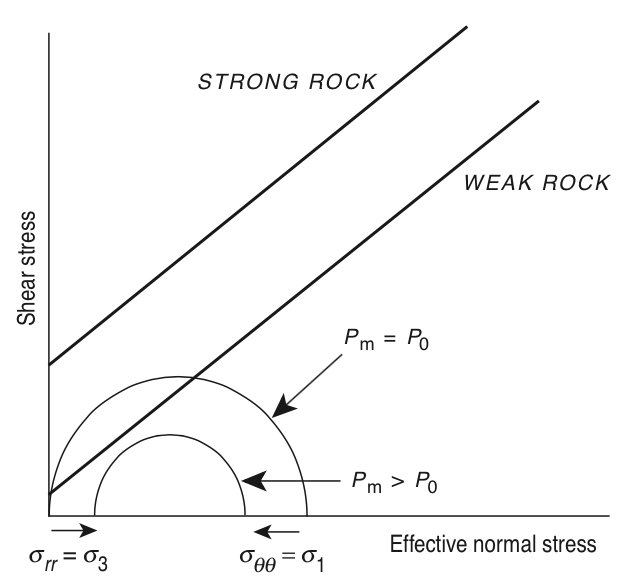
Pressure dependence

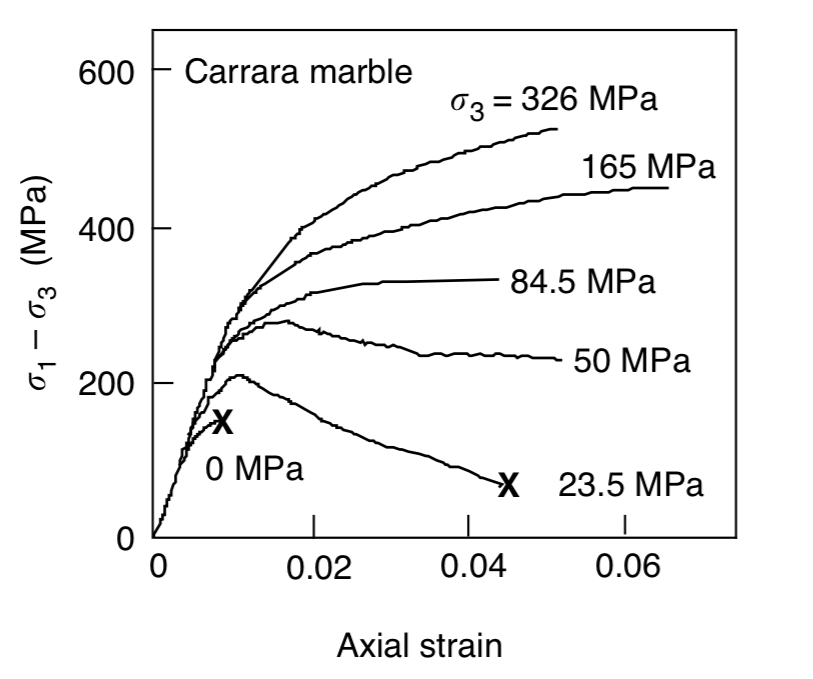
© Blackwell Publishing Jaeger, et al., Fundamentals of Rock Mechanics (Fig. 4.5, pp. 86)

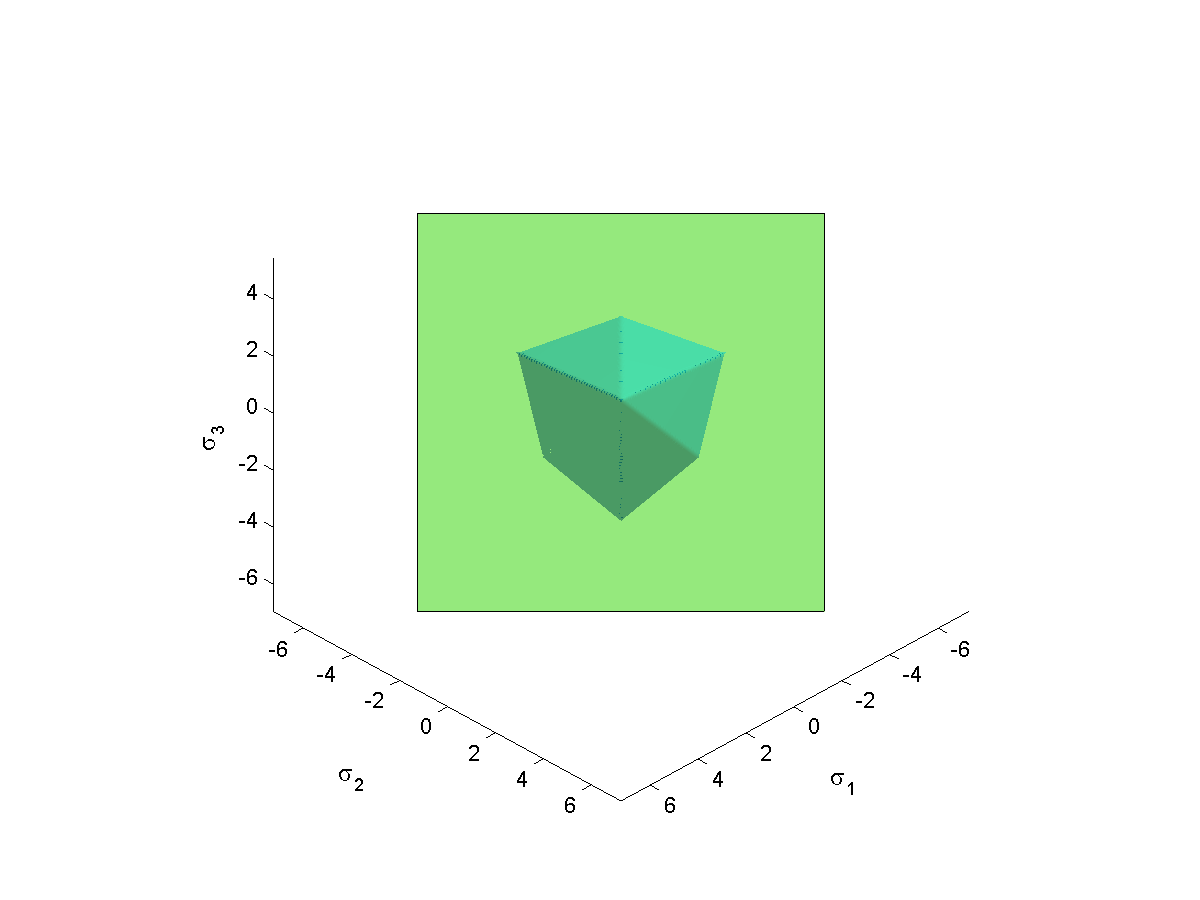
Other failure criteria

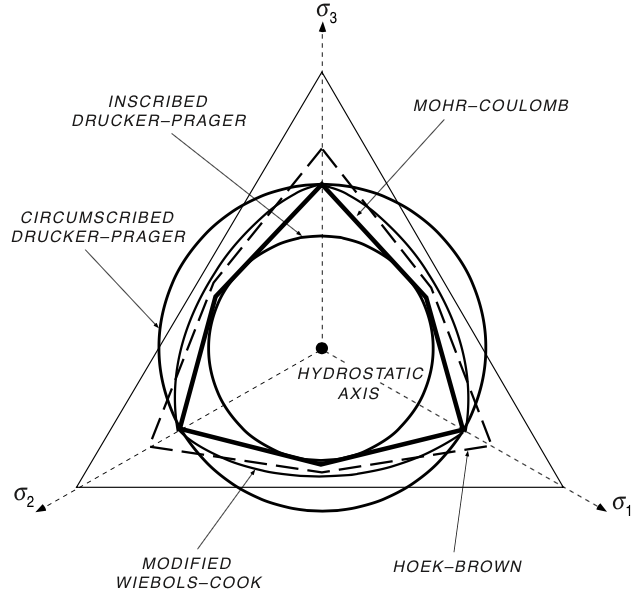
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.6, pp. 94)

Recall: Mohr Envelope for Sandstone

${}$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.3a, pp. 88)

Hoek-Brown criterion (parabolic fitting)

${}$

$$ \sigma_1 = \sigma_3 + C_0 \sqrt{m \dfrac{\sigma_3}{C_0} + s} $$

$m$ and $s$ are fitting parameters that depend on rock properties and the degress of fracturing. Typical values

Typical Range of $ m $	Types of rocks
$5 < m < 8$	carbonate rocks (dolomite, limestone, marble)
$4 < m < 10$	lithified argillaceous rocks (sandstones, quartizite)
$15 < m < 24$	arenaceous rocks (andesite, dolerite, diabase, rhyolite)
$22 < m < 33$	course-grained polyminerallic gineous and metamorphic (amphibolite, gabbro, gneiss, norite, quartz-diorite)

Intact Rocks -- $s \to 1$

Completely Granualated -- $s \to 0$

Lade Criterion

${}$

$$ \left( \frac{I_1^3}{I_3} - 27 \right) \left( \frac{I_1}{p_a} \right)^{m'} = \eta_1 $$

with

$I_1 = S_{ii} = S_1 + S_2 + S_3$ (first invariant of $\mathbf{S}$)

$I_3 = \det(\mathbf{S}) = S_1 S_2 S_3$ (third invariant of $\mathbf{S}$)

$p_a$ is atmospheric pressure, $m'$ and $n_1$ are material constants

Modified Lade Criterion (dependece on $\sigma_2$)

${}$

$$ \left( \frac{(I_1')^3}{I_3'} \right) = 27 + \eta $$

with

$I_1' = (\sigma_1 + S) + (\sigma_2 + S) + (\sigma_3 + S)$

$I_3' = (\sigma_1 + S) (\sigma_2 + S) (\sigma_3 + S)$

$S = \dfrac{S_0}{\tan\phi}$

$\eta = \dfrac{4 (\tan\phi)^2 (9- 7 \sin\phi)}{1 - \sin \phi)}$

$\tan\phi = \mu_i$ and $S_0$ from Mohr-Coulomb criterion

Comparison

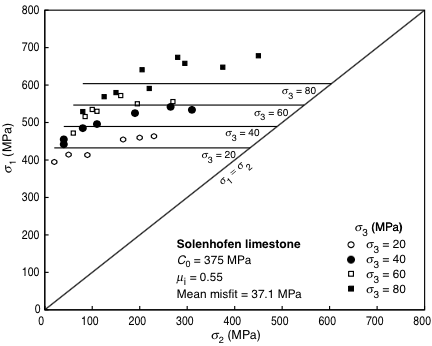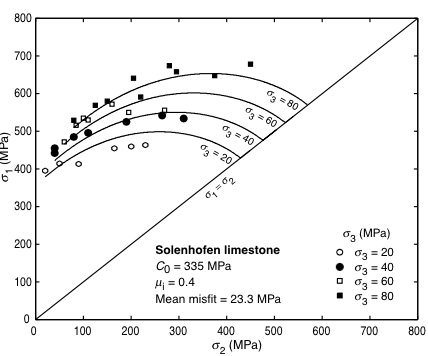Mohr-Coulomb	modified Lade

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.8b and 4.9b, pp. 96-97)

Others

• modified Wiebols-Cook
• Druker-Prager
• many more!

Strength anisotropy

$$ \sigma_1 = \sigma_3 \frac{2 (S_w + \mu_w \sigma_3)}{(1-\mu_w \cot\beta_w)\sin 2\beta} $$

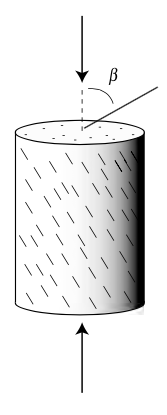
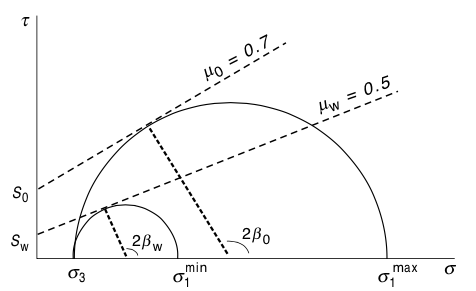
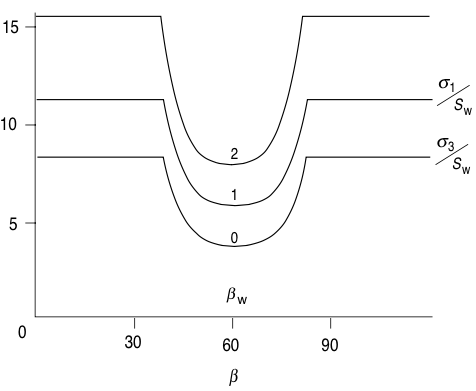
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.12, pp. 106)

Recall: Yield surface

Mohr Coulomb Yield Surface 3Da. Licensed under CC BY-SA 3.0 via Wikipedia

Shear enhanced compaction

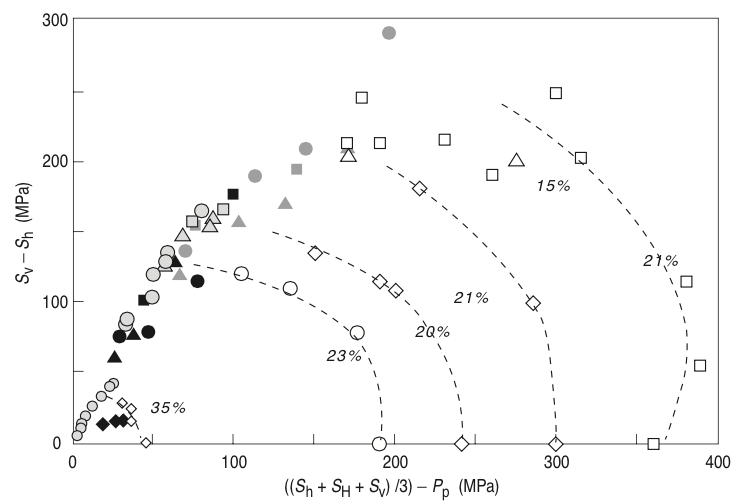Porosity loss in sandstone

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.20, pp. 120)

Cam-Clay model

${}$

$$ M^2 p^2 - M^2 p_0 p + q^2 = 0 $$

with

$$ p = \dfrac{1}{3}\left(\sigma_1 + \sigma_2 + \sigma_3\right) $$$$ q^2 = \dfrac{1}{2} \left((S_1 - S_2)^2 + (S_2 - S_3)^2 + (S_1 - S_3)^2 \right) $$$$ M = \dfrac{q}{p} $$

Cam-Clay model

${}$

Sandia geomodel (Kayenta)

${}$

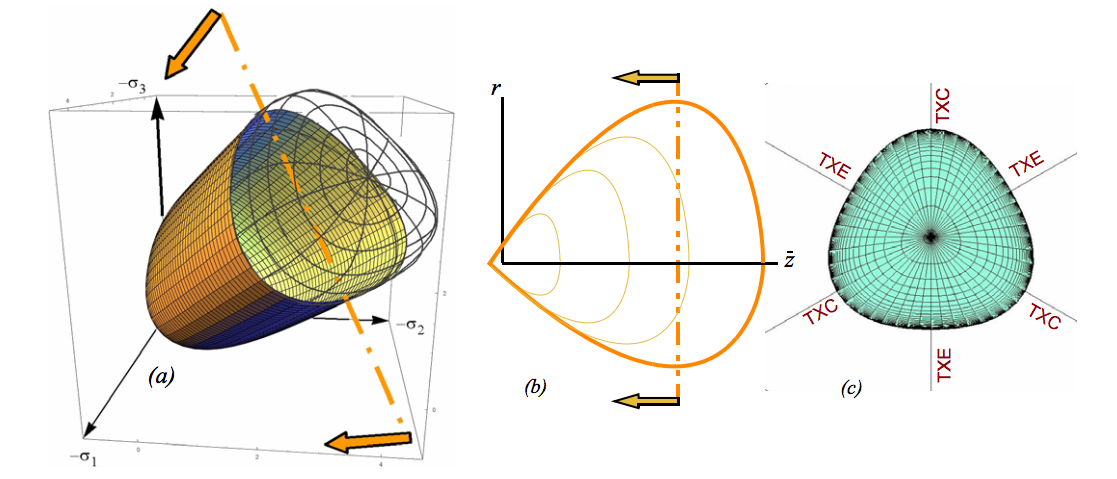
R.M. Brannon, A.F. Fossum, and O.E. Strack: Kayenta: Theory and User’s Guide. Tech. rep. Sandia National Laboratories, 2009.