Tensile strength of rocks

• Relatively unimportant!

• Reasons:

  • Tensile strength is low compared to compressive strength.

  • When a large enough volume of rock is considered, flaws are bound to exist making the tensile strength near zero.

  • In situ stress at depth is never tensile.

Opening mode fracture (Mode I)

${}$

$$ K_{Ic} \ge K_I = (P_f - S_3) \pi \sqrt{L} $$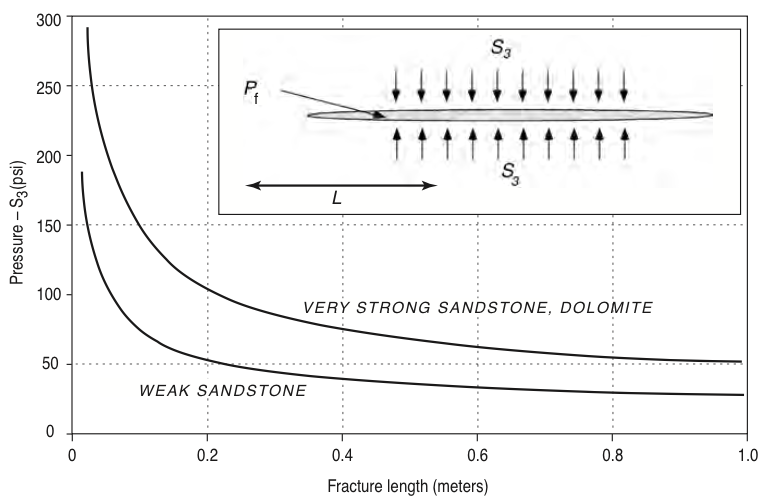

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.21, pp. 122)

Recall: Slip on faults

${}$

$$ \dfrac{\tau}{\sigma_n} = \mu $$

Coulomb failure function

$$ f = \tau - \mu \sigma_n \le 0 $$

Critically stressed crust

${}$

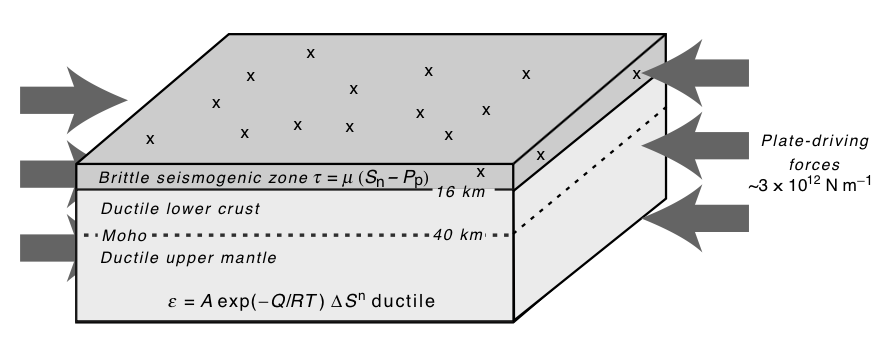
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.25, pp. 129)

Stress magnitudes controlled by frictional strength

${}$

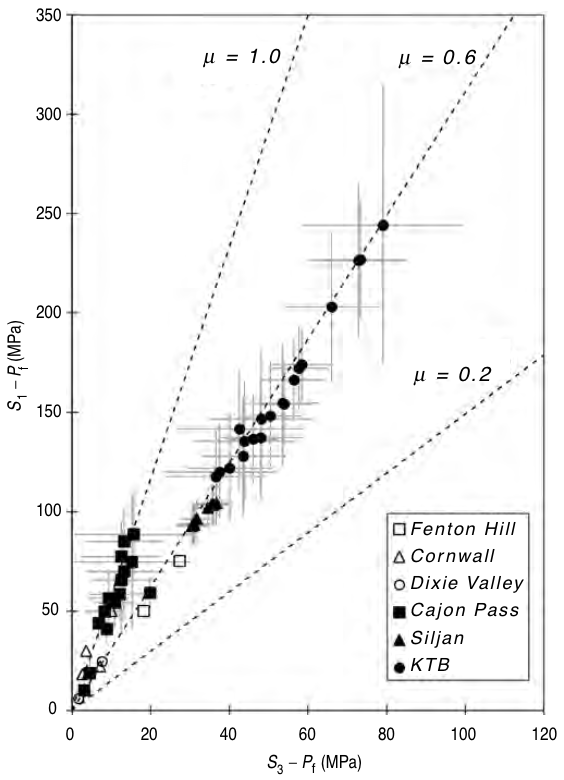
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.26, pp. 129)

Limits on in situ stress

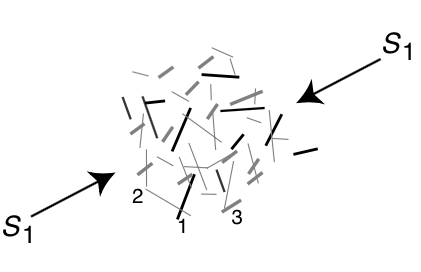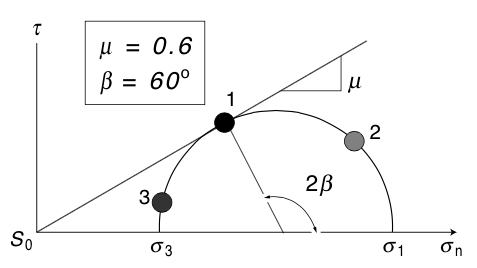Optimal angle for frictional sliding:

$$ \beta = \frac{\pi}{4} + \frac{1}{2} \tan^{-1}\mu $$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.27b,c, pp. 131)

Principle stress ratio

${}$

$$ \frac{\sigma_1}{\sigma_3} = \frac{S_1 - P_p}{S_3 - P_p} = \left(\sqrt{\mu^2 + 1}+\mu^2\right)^2 $$

Asuming $\mu = 0.6$

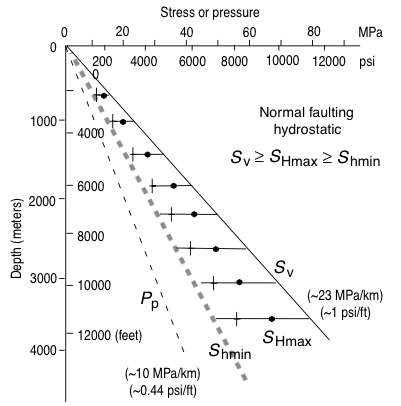
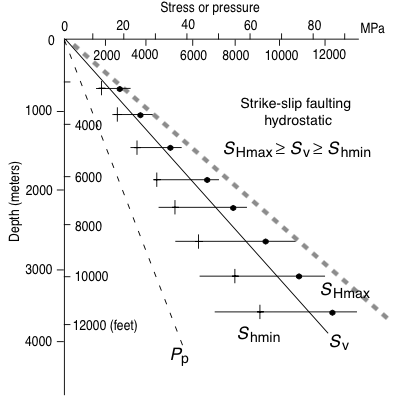
$$ \frac{\sigma_1}{\sigma_3} = 3.1 $$

Stress bounds

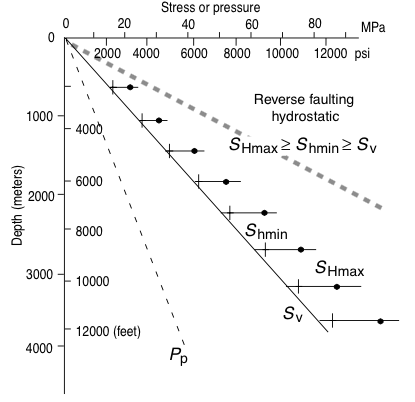$\dfrac{S_v - P_p}{S_{hmin} - P_p} \le \left(\sqrt{\mu^2 + 1}+\mu^2\right)$	$\dfrac{S_{Hmax} - P_p}{S_{hmin} - P_p} \le \left(\sqrt{\mu^2 + 1}+\mu^2\right)$	$\dfrac{S_{Hmax} - P_p}{S_v - P_p} \le \left(\sqrt{\mu^2 + 1}+\mu^2\right)$

Pore pressure, stress difference, and fault slip

${}$

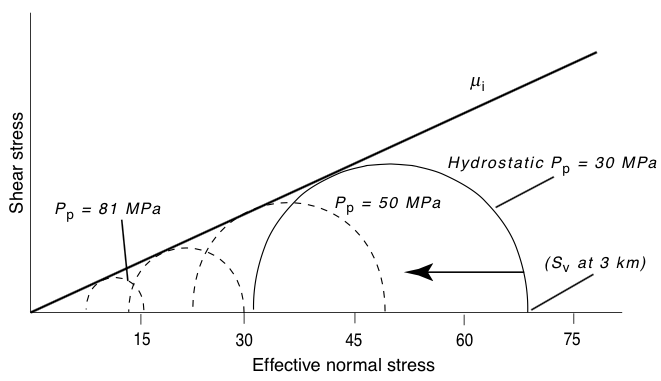
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.30, pp. 136)