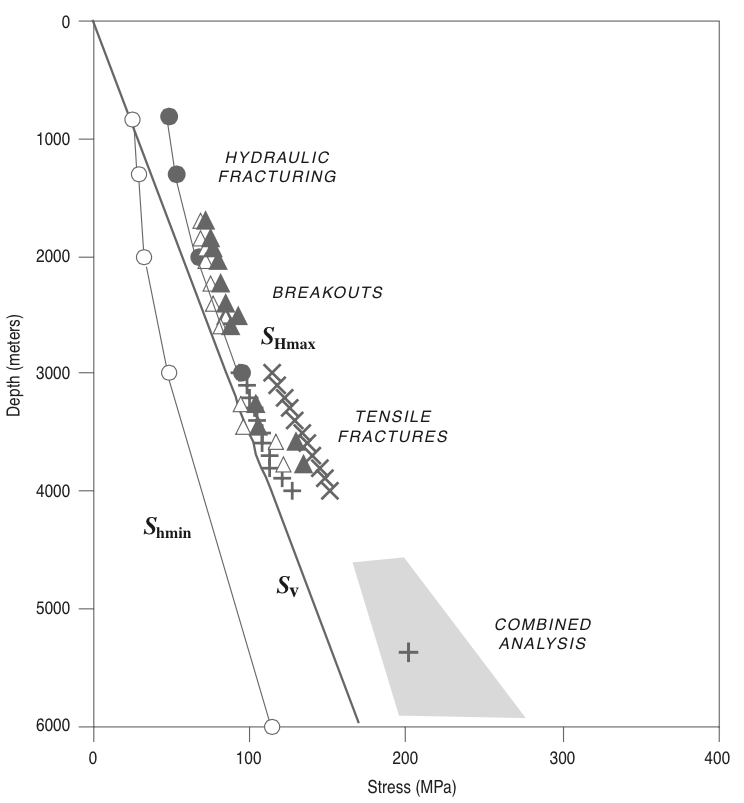
Compressive and tensile failure in vertical wells

Stress around circular cavity

$${}$$

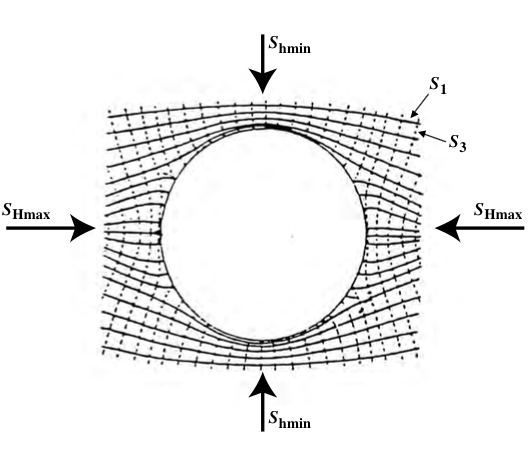
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.1, pp. 169)

Kirsch solution

${}$

\begin{align} \sigma_{rr} &= \frac{ \sigma_{Hmax} + \sigma_{hmin} }{2}\left( 1 - \frac{a^2}{r^2} \right) + \frac{ \sigma_{Hmax} - \sigma_{hmin} }{2}\left( 1 - 4 \frac{a^2}{r^2} + 3 \frac{a^4}{r^4}\right)\cos 2\theta + (P_w-P_p)\left(\frac{a^2}{r^2}\right) \\ \sigma_{\theta\theta} &= \frac{ \sigma_{Hmax} + \sigma_{hmin} }{2}\left( 1 + \frac{a^2}{r^2} \right) - \frac{ \sigma_{Hmax} - \sigma_{hmin} }{2}\left( 1 + 3 \frac{a^4}{r^4}\right)\cos 2\theta - (P_w-P_p)\left(\frac{a^2}{r^2}\right) \\ \sigma_{r\theta} &= \frac{ \sigma_{Hmax} - \sigma_{hmin} }{2}\left( 1 + 2\frac{a^2}{r^2} - 3 \frac{a^4}{r^4} \right) - \sin 2\theta \\ \sigma_{zz} &= \sigma_v - 2 \nu (\sigma_{Hmax} -\sigma_{hmin})\left(\frac{a^2}{r^2}\right)\cos 2 \theta \end{align}

Example

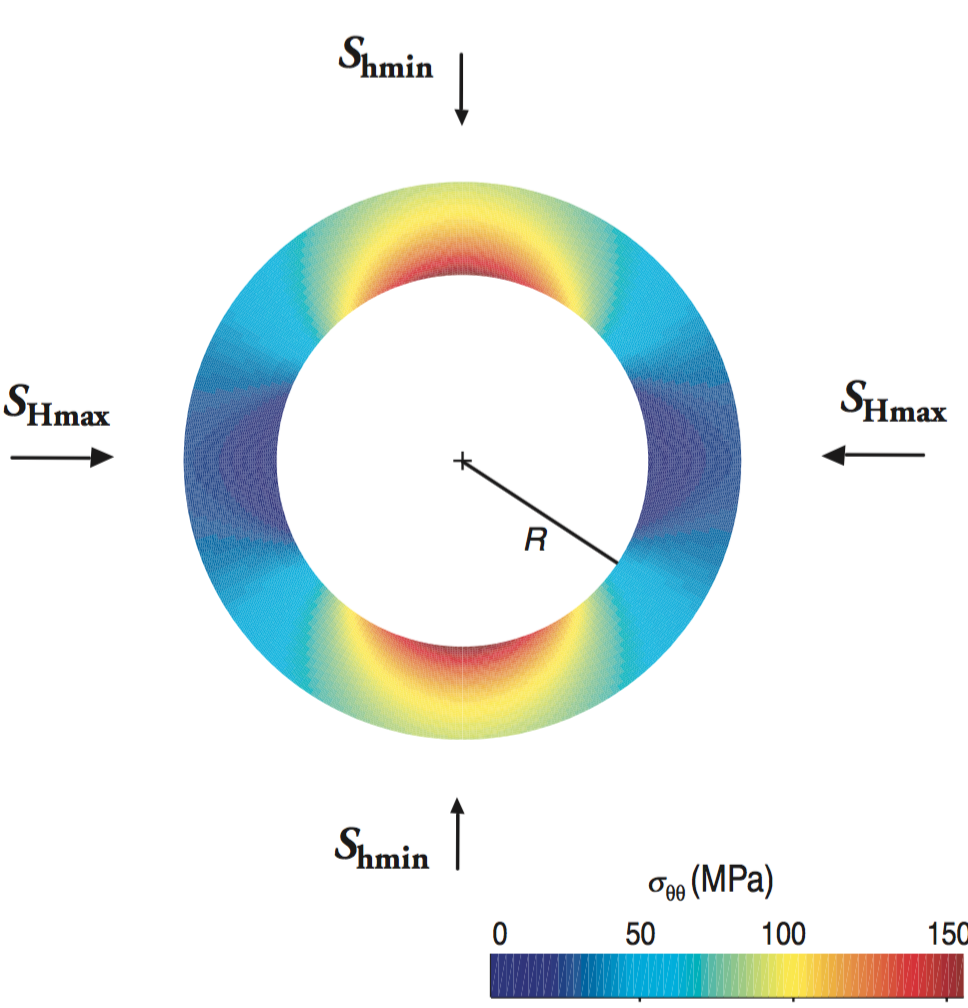$$\quad \quad \quad \quad$$

\begin{align} S_{Hmax} &= 90 \mbox{MPa} \\ S_{v} &= 88.2 \mbox{MPa} \\ S_{hmin} &= 51.5 \mbox{MPa} \\ P_{p} &= 31.5 \mbox{MPa} \\ P_{w} &= 31.5 \mbox{MPa} \end{align}

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.2a, pp. 171)

${}$

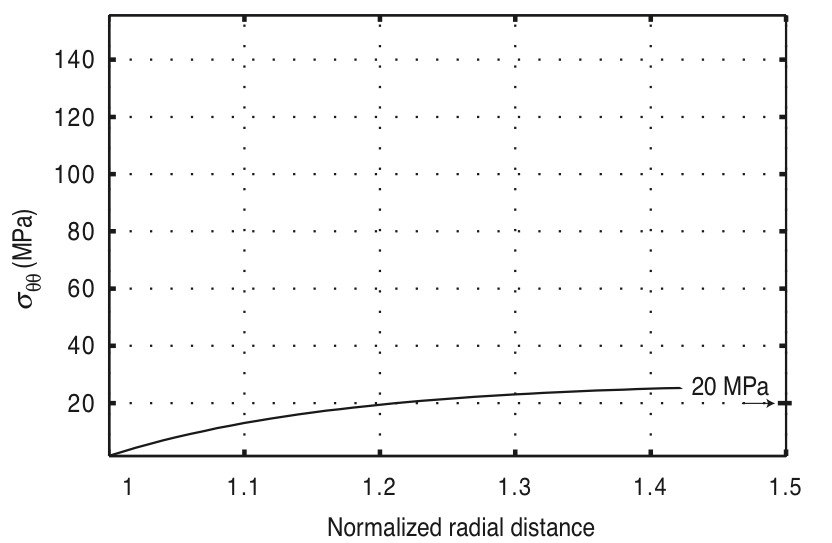	$$\quad$$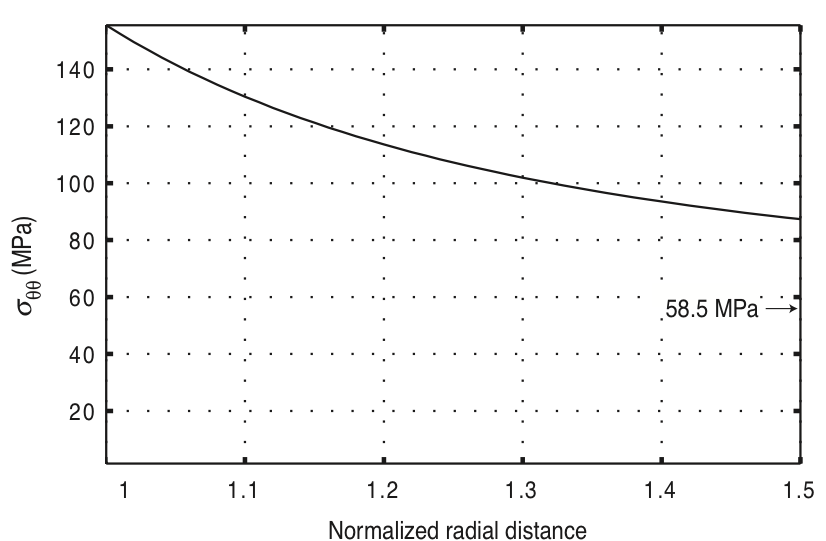
Along azimuth of $S_{Hmax}$	$$\quad$$	Along azimuth of $S_{hmin}$

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.2b,c, pp. 171)

Variation of wellbore stresses

${}$

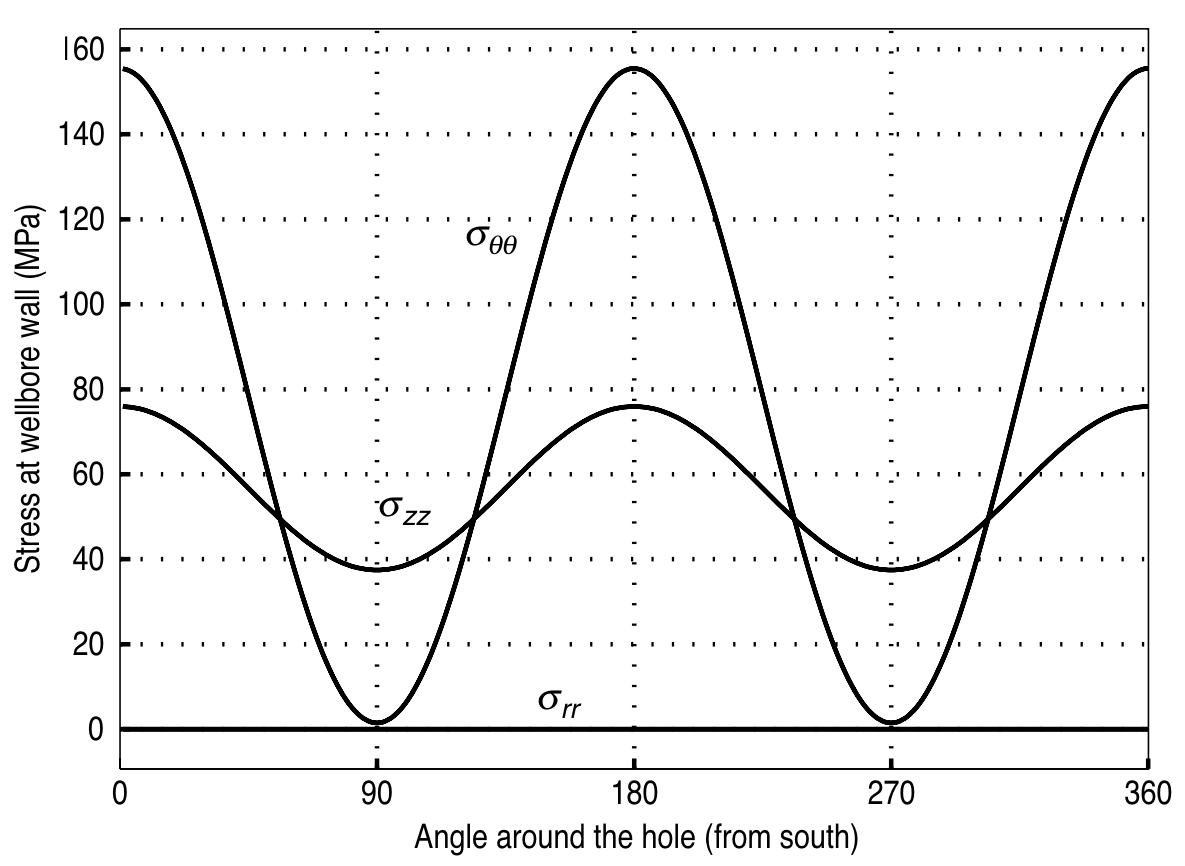
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.3a, pp. 173)

Wellbore breakout region

${}$

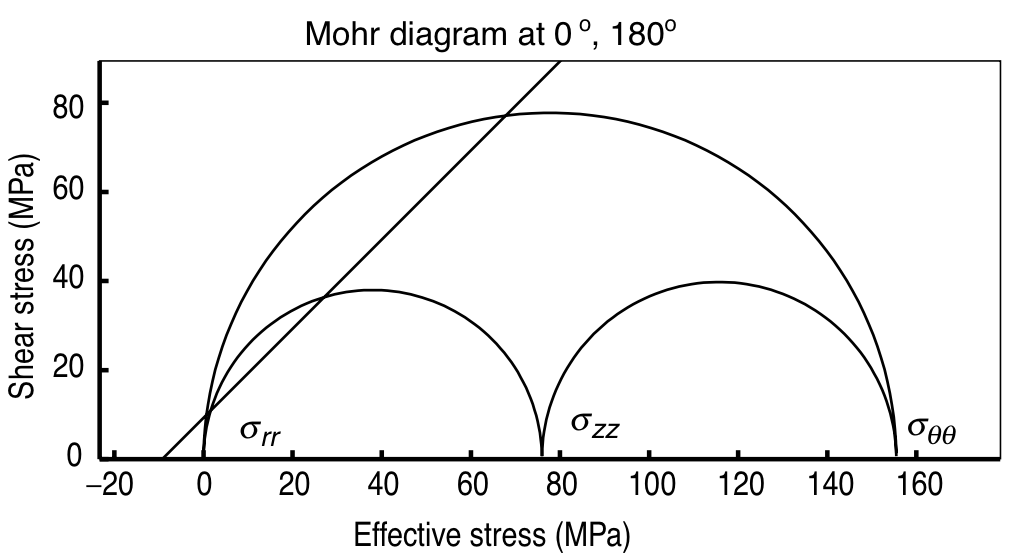$$\quad$$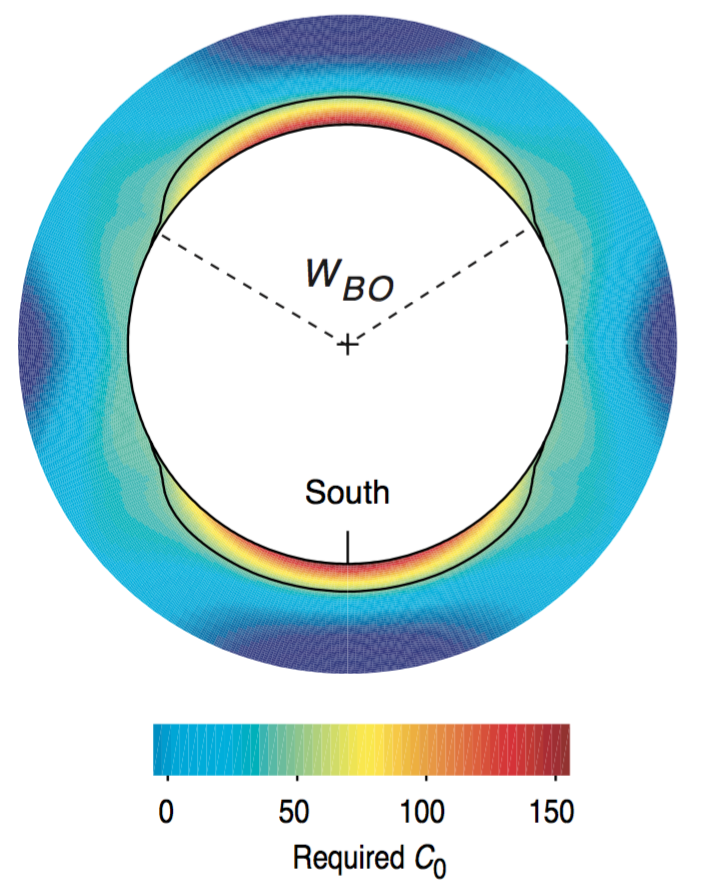

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.3b,c, pp. 173)

Mudweight stabilization

As $\Delta P$ increases, $\sigma_{\theta\theta}$ decreases and $\sigma_{rr}$ increases.

$$\quad$$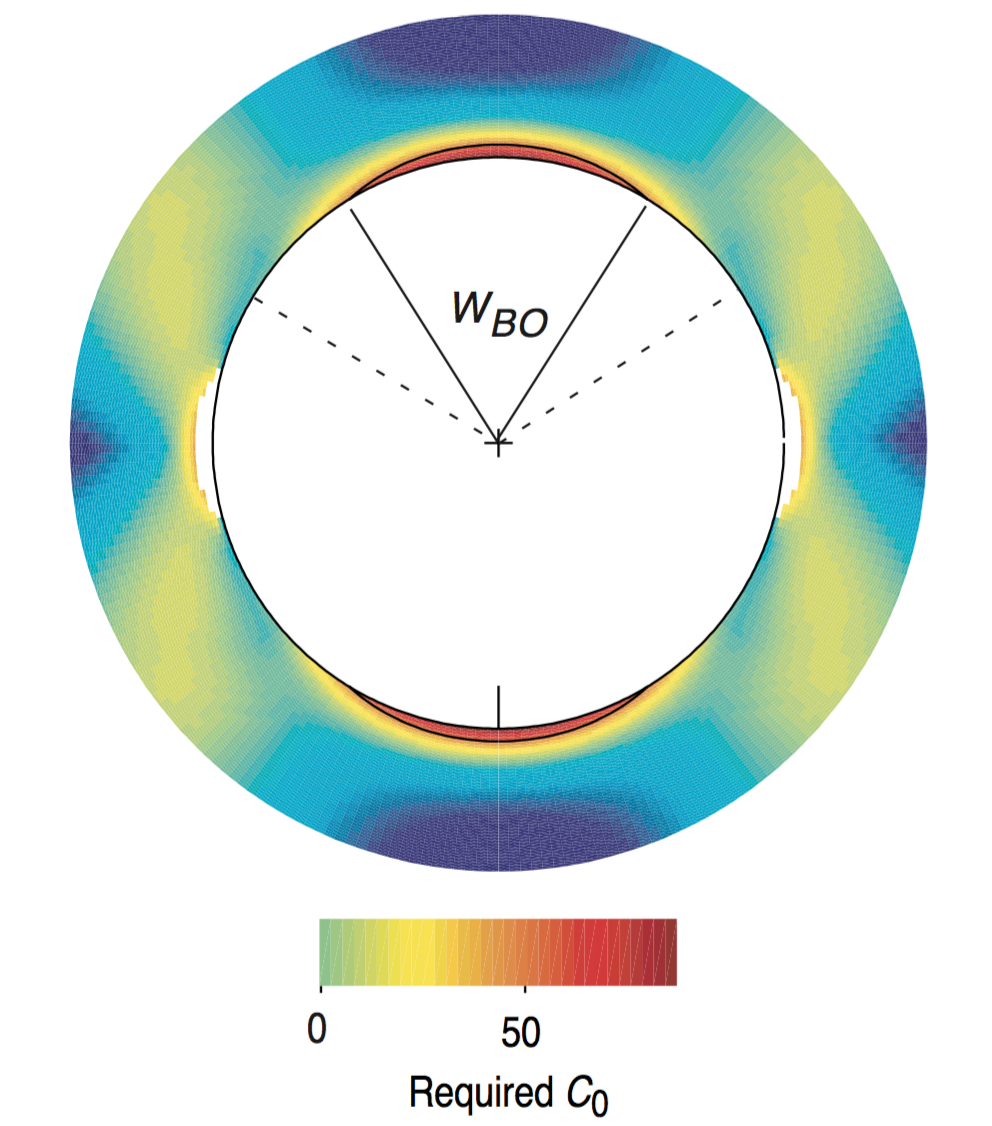

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.3b, pp. 173 and Fig. 6.5a, pp. 177)

Breakouts as indicators of far-field stresses

Simplify Kirsch equations at wellbore wall $a = r$, so

\begin{align} \sigma_{rr} &= (P_w-P_p) = \Delta P \\ \sigma_{\theta\theta} &= \sigma_{Hmax} + \sigma_{hmin} - 2 (\sigma_{Hmax} - \sigma_{hmin} ) \cos 2 \theta - \Delta P \\ \sigma_{zz} &= \sigma_v - 2 \nu (\sigma_{Hmax} -\sigma_{hmin})\cos 2 \theta \end{align}

$\sigma_{\theta\theta}$ has min at 0$^\circ$ and 180$^\circ$

\begin{align} \sigma_{\theta\theta}^{min} &= 3\sigma_{Hmin} - \sigma_{Hmax} - \Delta P \\ \end{align}

$\sigma_{\theta\theta}$ has max at 90$^\circ$ and 270$^\circ$, so

\begin{align} \sigma_{\theta\theta}^{max} &= 3\sigma_{Hmax} - \sigma_{hmin} - \Delta P \\ \end{align}

so

\begin{align} \sigma_{\theta\theta}^{max} - \sigma_{\theta\theta}^{min} &= 4(\sigma_{Hmax} - \sigma_{hmin}) \end{align}

Tensile induced fractures

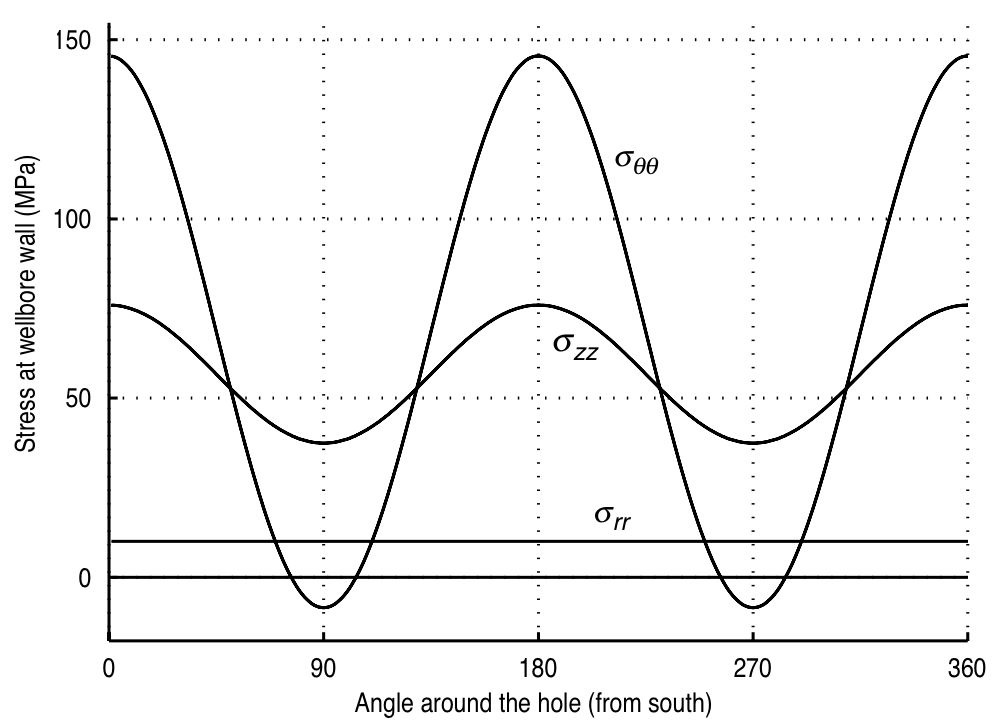
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.5a, pp. 177)

Safe drilling mud window

• Mud weight too low

  • Breakouts

• Mud weight too high

  • Tensile induced fractures leading to lost circulation

Imaging breakouts

${}$

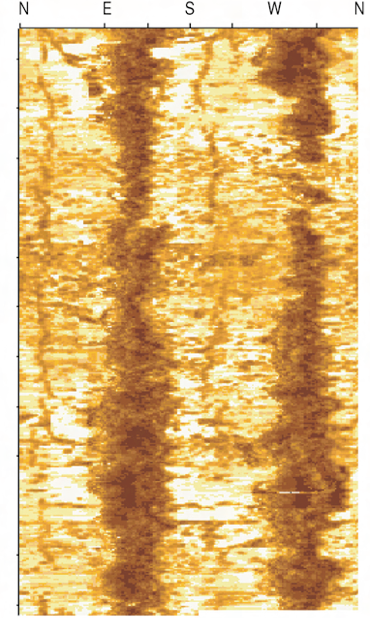	$$\quad$$		$$\quad$$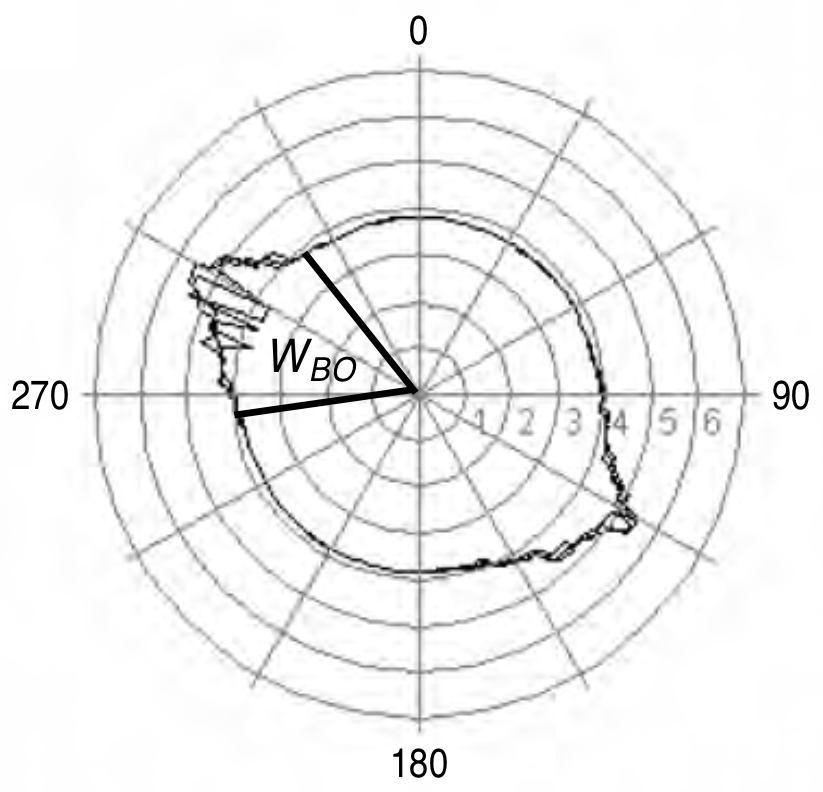
Ultrasonic $P$-wave	$$\quad$$	Electrical resistivity	$$\quad$$	Breakout cross-section

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.4a,b,c, pp. 176)

Four-arm caliper data

${}$

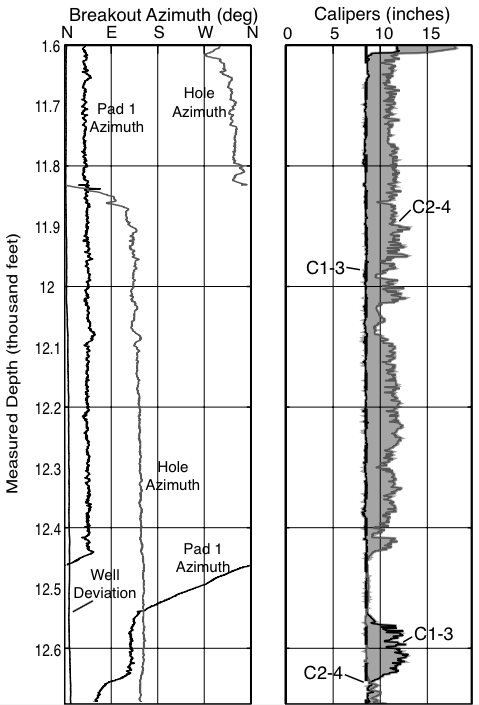	$$\quad$$		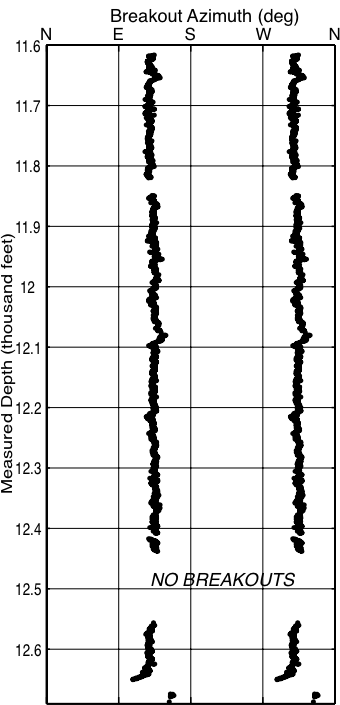$$\quad$$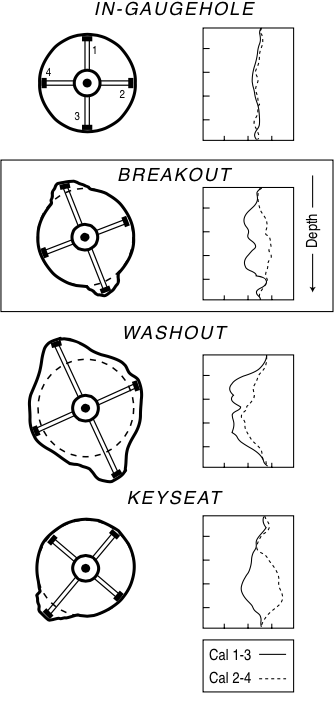
Caliper data	$$\quad$$	Breakout indication	$$\quad$$	Examples of variations

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.9a,b,c, pp. 183)

Thermal effects on wellbore stress

${}$

Strongly time dependent

$$ \frac{\partial T}{\partial t} = \alpha_T \nabla^2 T $$

$\alpha \to$ strongly depenendent of the silica content of the rock.

Under steady-state conditions,

$$ \Delta \sigma_{\theta\theta}^T = \frac{\alpha_T E \Delta T}{1-\nu} $$

Time-temperature effects

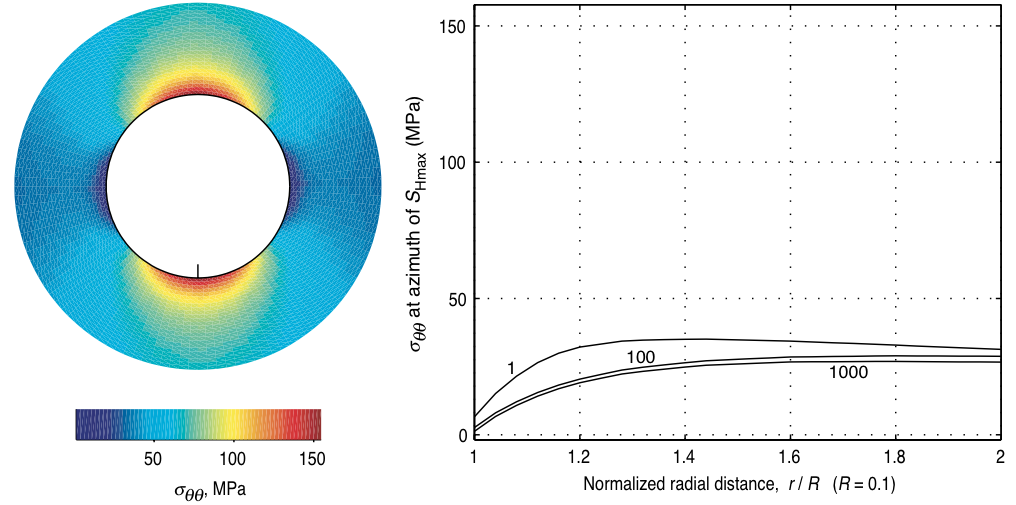	\begin{align}\Delta T =& 25^{\circ} \mbox{ C} \\ \Delta P =& 6 \mbox{ MPa}\end{align}

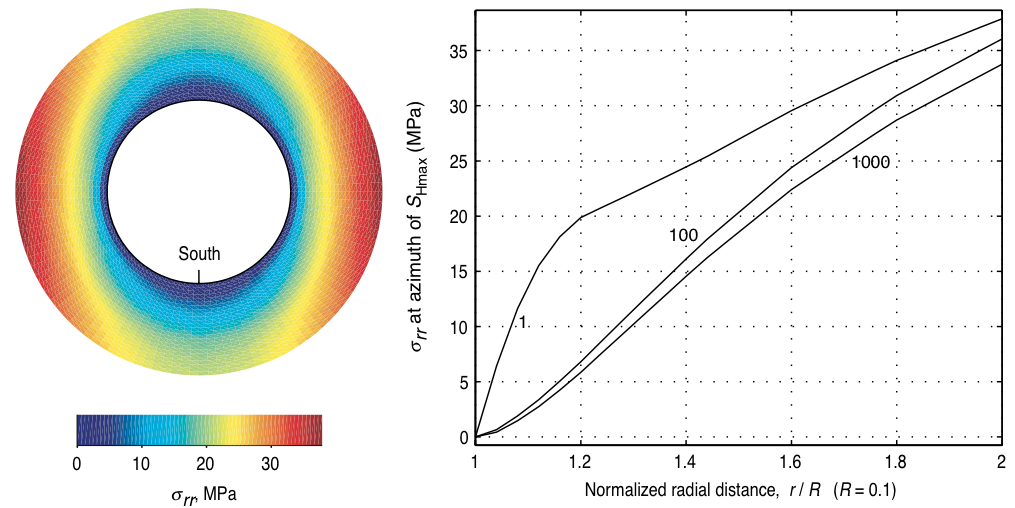© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.14a,b pp. 194)

Stability through cooling?

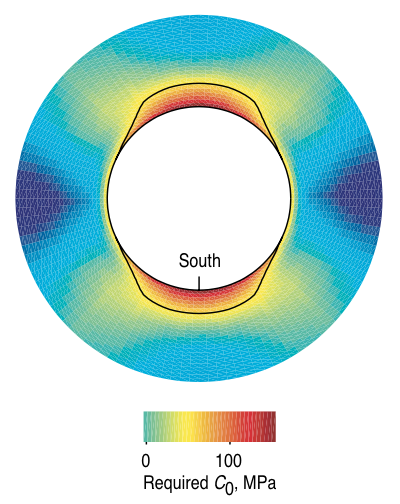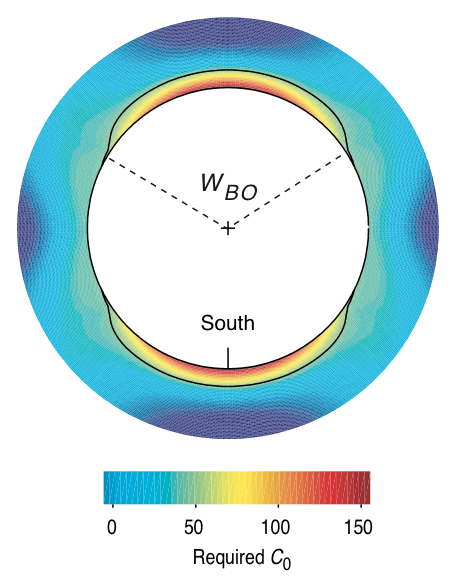Cooling	Reference

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.14c pp. 194 and Fig. 6.3 pp. 173)

Rock strength anisotropy

$$ \sigma_1 = \sigma_3 \frac{2 (S_w + \mu_w \sigma_3)}{(1-\mu_w \cot\beta_w)\sin 2\beta} $$

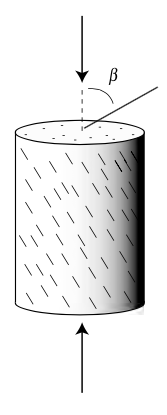
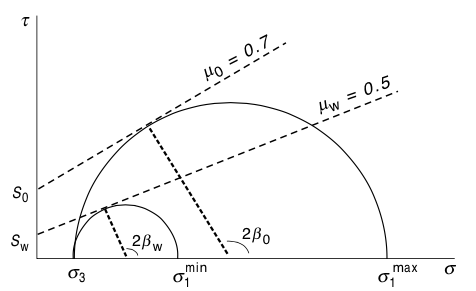
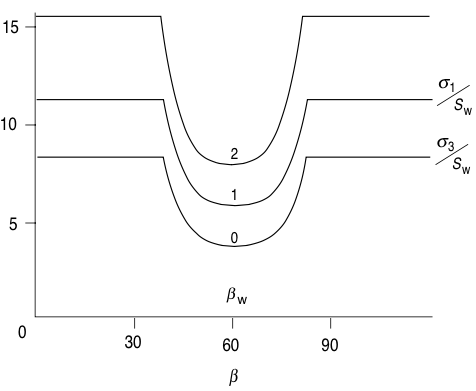
© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 4.12, pp. 106)

Rock strength anisotropy effects on breakouts

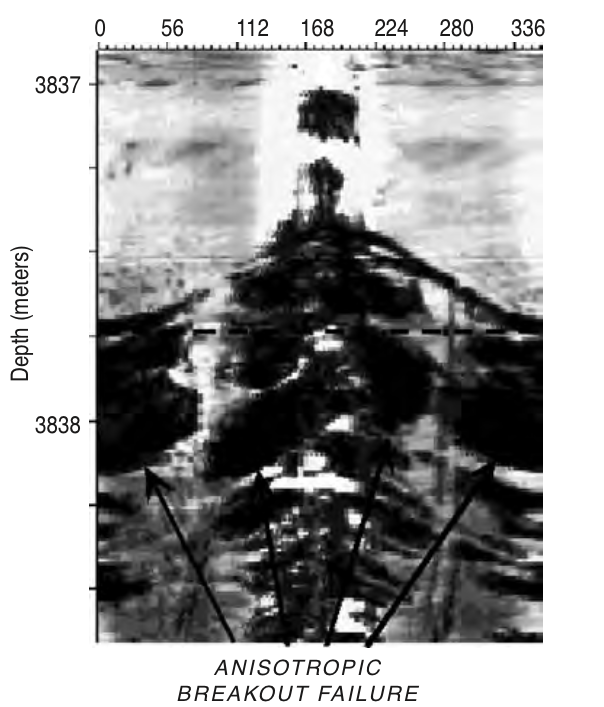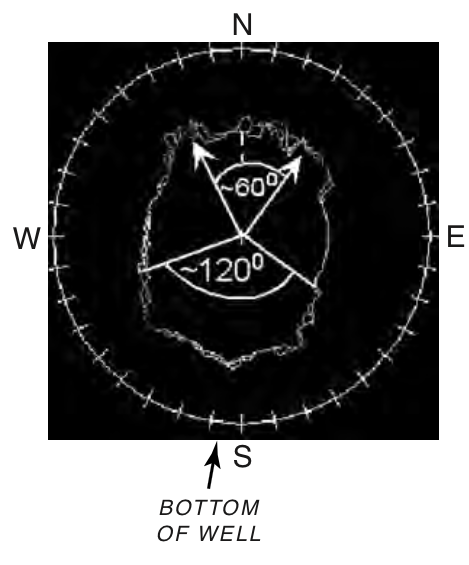© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.16a,b pp. 199)

Two mechanisms

• Stresses exceed intact rock strength

• Stresses activate slip on weak bedding planes

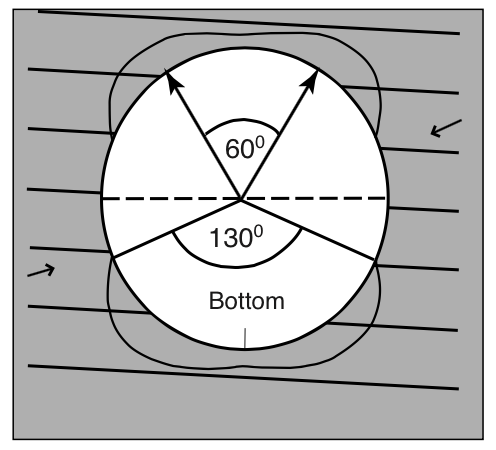© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 6.16c pp. 199)

Chemical effects

• Water Activity ($A_w \sim \frac{1}{\mbox{salinity}}$) can to increased pore pressure

$S_{Hmax}$ from breakout data

${}$

$$ S_{Hmax} = \frac{(C_0 + 2 P_p + \Delta P + \Delta \sigma^T) - S_{hmin}(1 + 2 \cos(\pi - w_{bo})}{1 - 2 \cos(\pi - w_{bo})} $$

Example

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 7.7 pp. 223)

Wellbore stability

Defining a "stable" wellbore

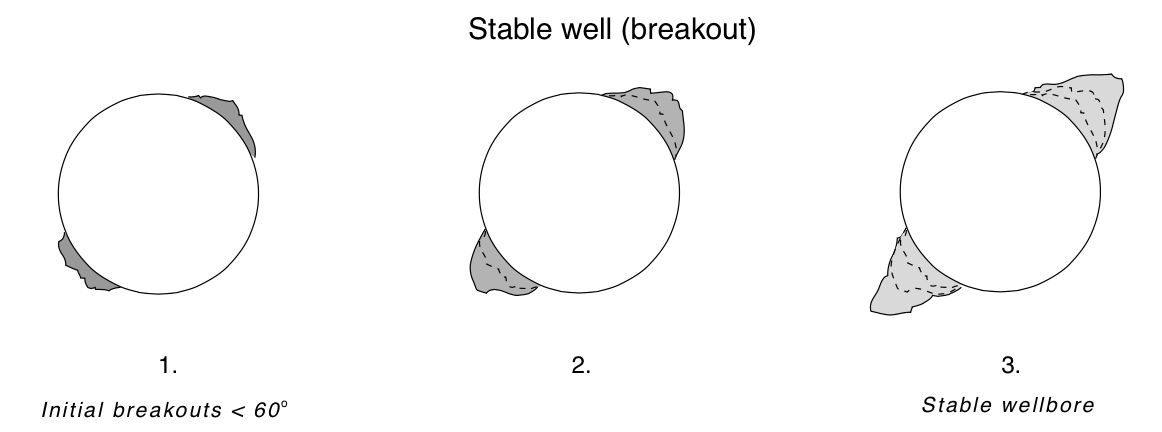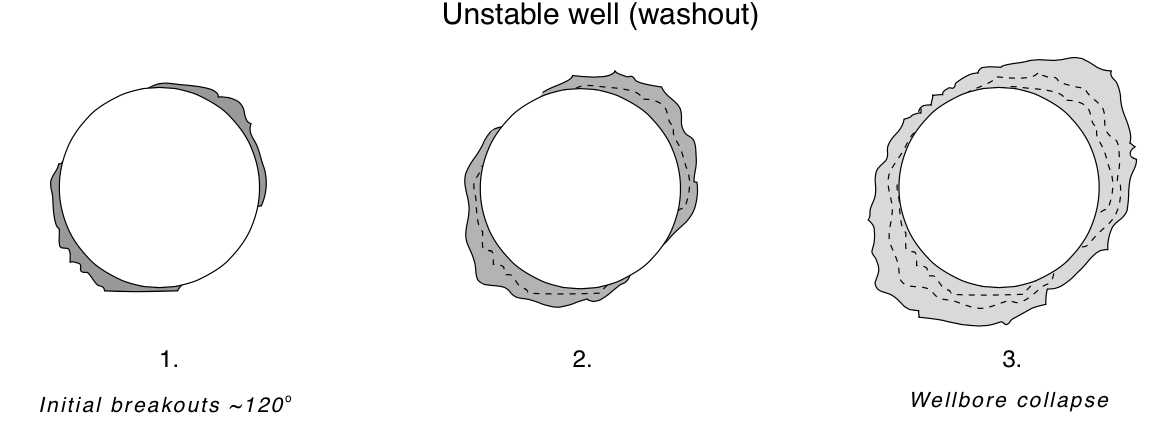© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 10.1a,b pp. 304)

Emperical model: Maximum 90$^{\circ}$ breakouts

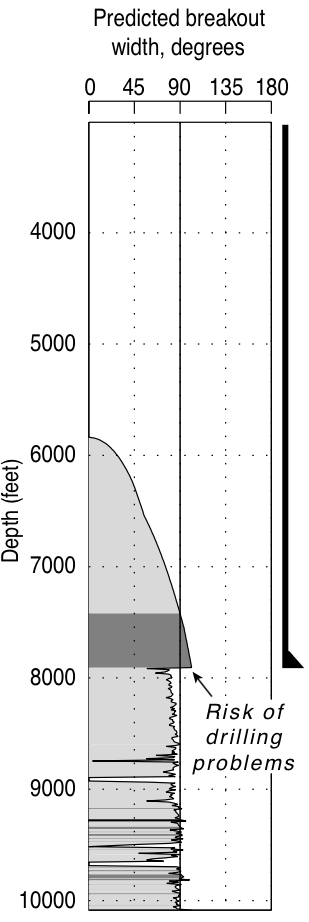$\quad \quad \quad \quad$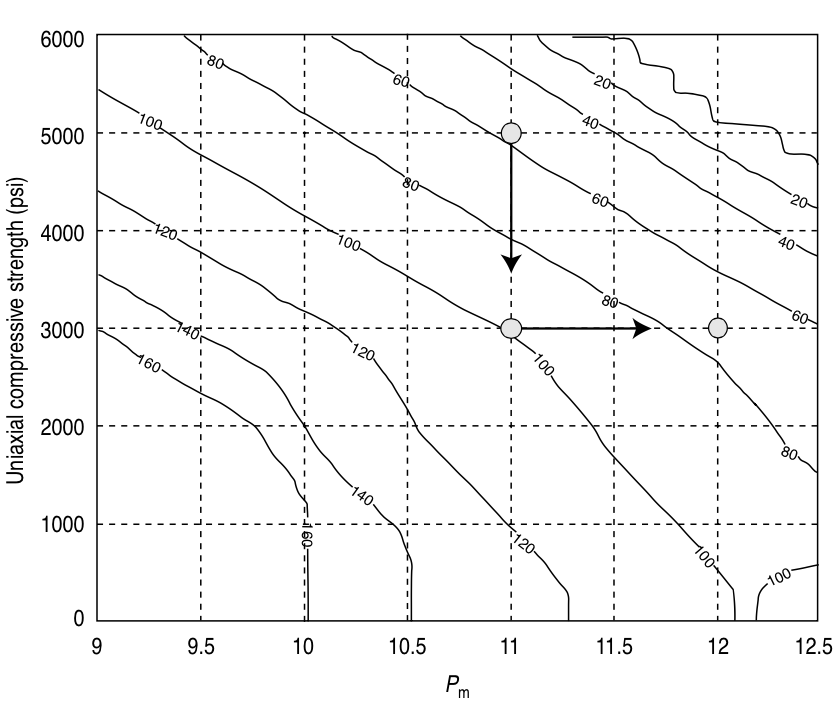

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 10.2a,b pp. 305)

Comprehensive model

i.e. why your studying geomechanics

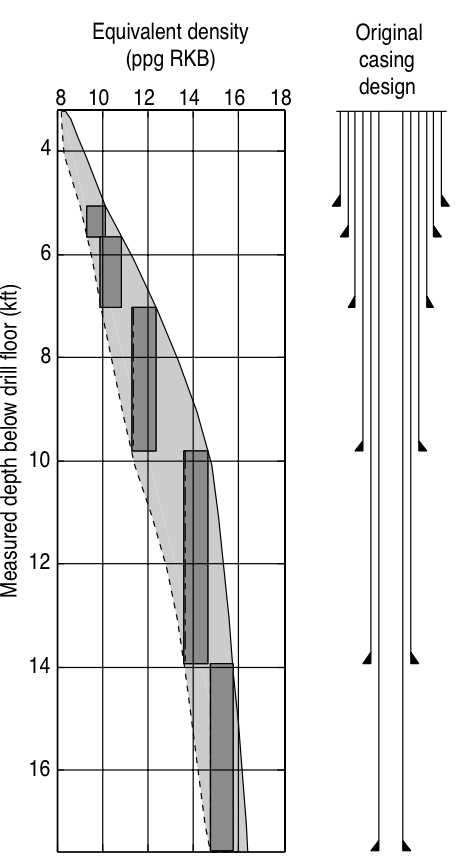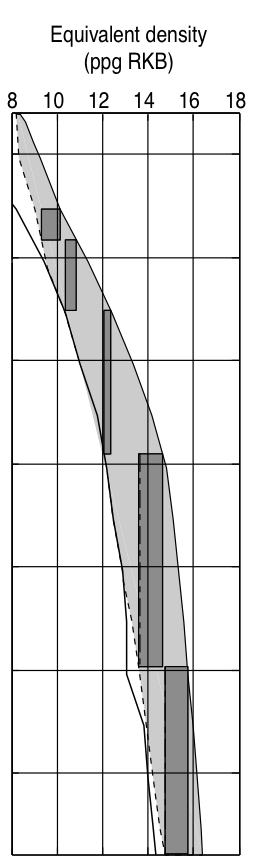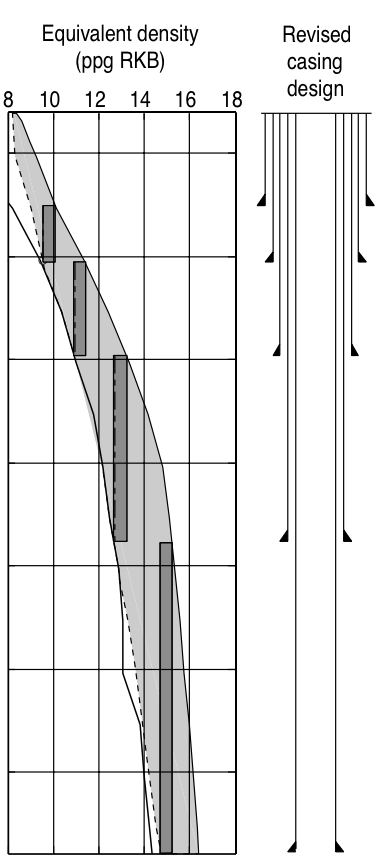Design based on pore pressure and frac gradient	Model considering collapse pressure	Final design

© Cambridge University Press Zoback, Reservoir Geomechanics (Fig. 10.3a,b,c pp. 307)