Kinematics of strain
Strain tensor
\[ \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{bmatrix} \]
\[\varepsilon_{ij} = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) \quad \mbox{for} \quad i=1,2,3 \quad j=1,2,3\]
Volumetric strain
\[ \varepsilon_{vol} = \mbox{tr}(\boldsymbol{\varepsilon}) = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} \]
Material constants for isotropic materials
Young’s modulus
\[E = \frac{S_{11}}{\varepsilon_{11}}\]
Bulk modulus
\[K = \frac{S_{11}+S_{22}+S_{33}}{3\varepsilon_{vol}}\]
Shear Modulus
\[G = \frac{1}{2} \frac{S_{13}}{\varepsilon_{13}}\]
Poisson’s ratio
\[\nu = \frac{\varepsilon_{33}}{\varepsilon_{11}}\]
Typical Young’s modulus values
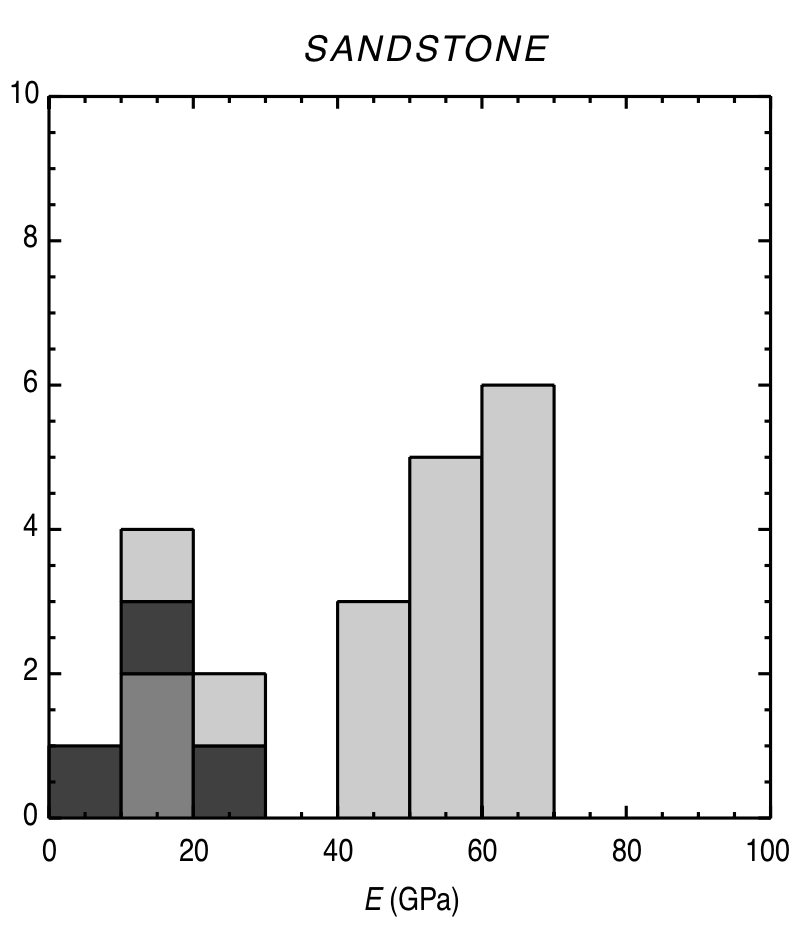
|
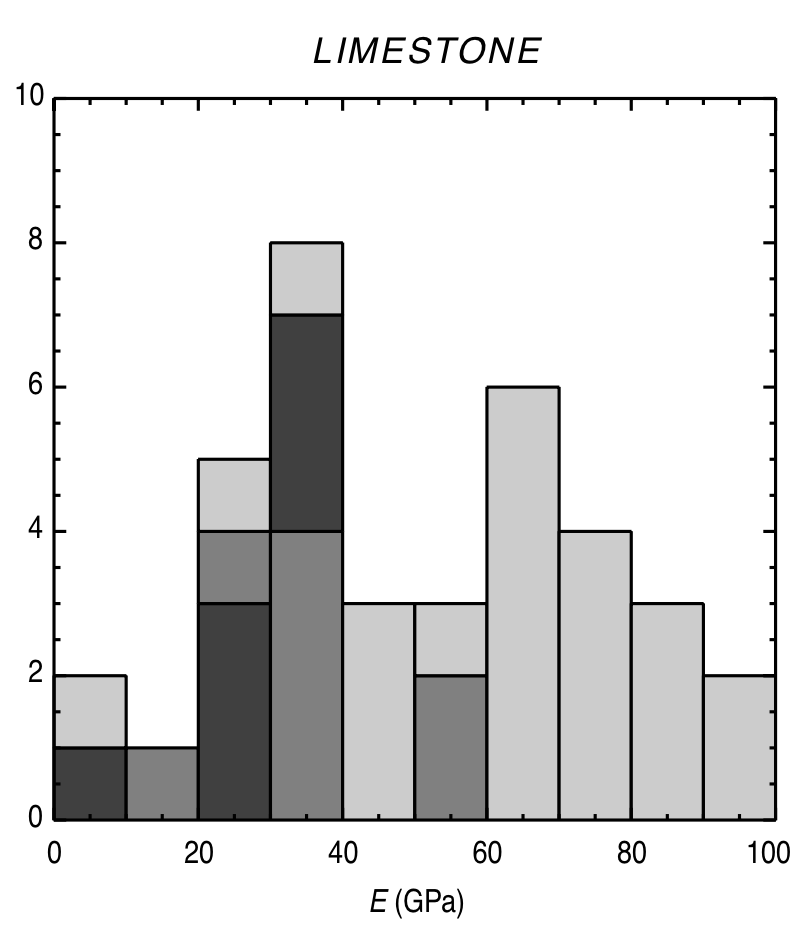
|
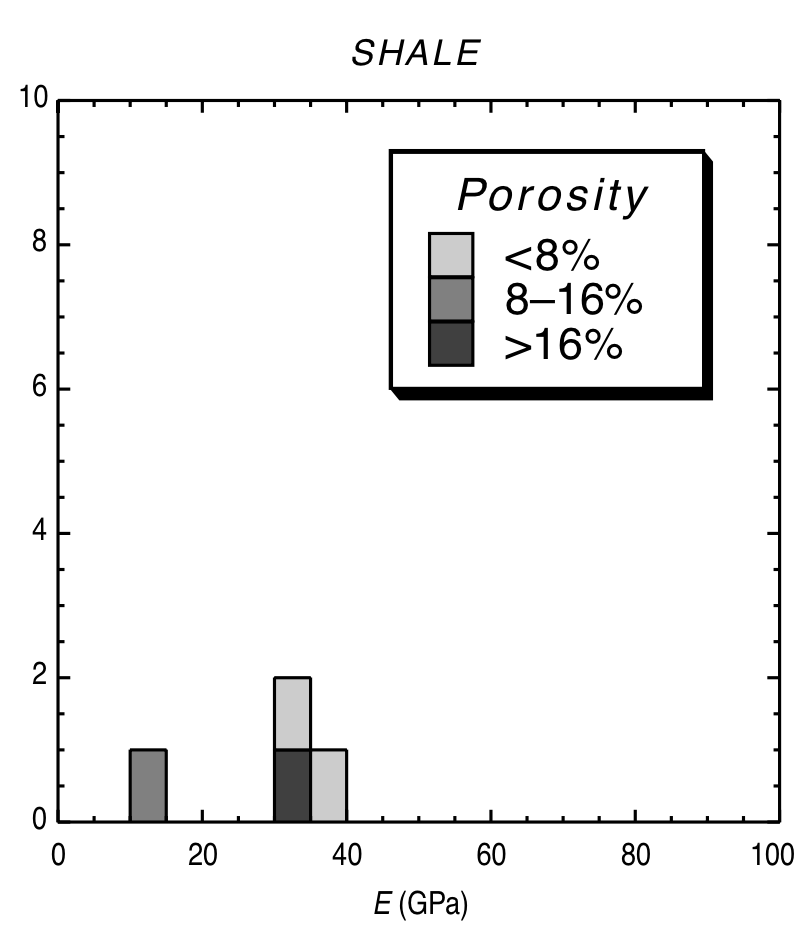
|
© Lama, R. D., and V. S. Vutukuri. HANDBOOK ON MECHANICAL PROPERTIES OF ROCKS-TESTING TECHNIQUES AND RESULTS. VOLUME 2. Monograph. 1978.)
Typical Poissons’ ratio values
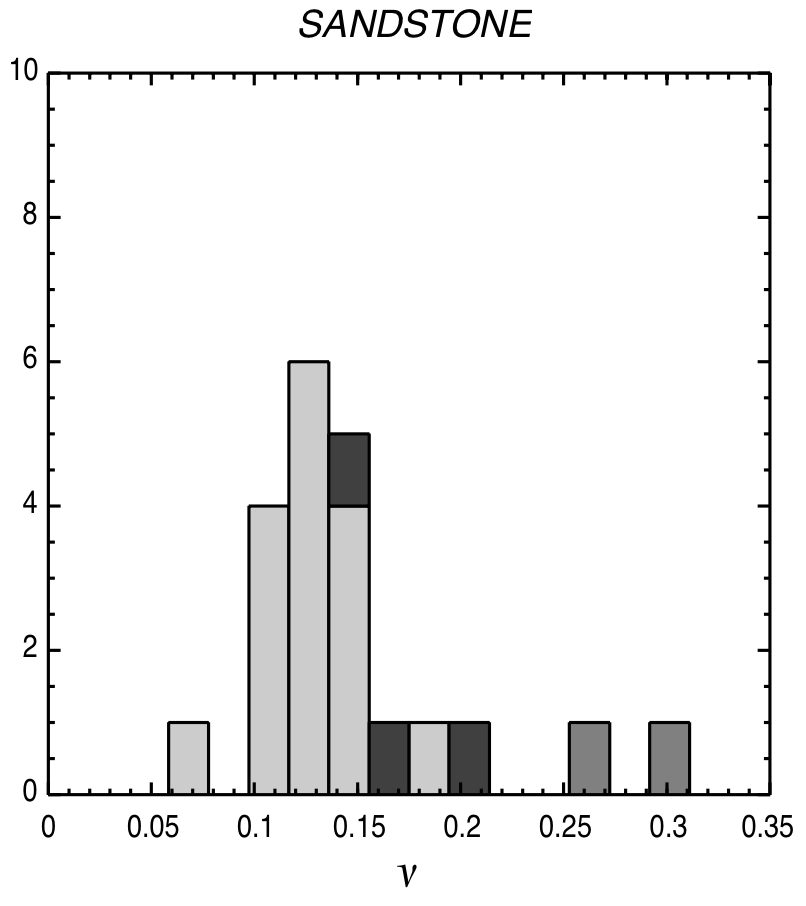
|
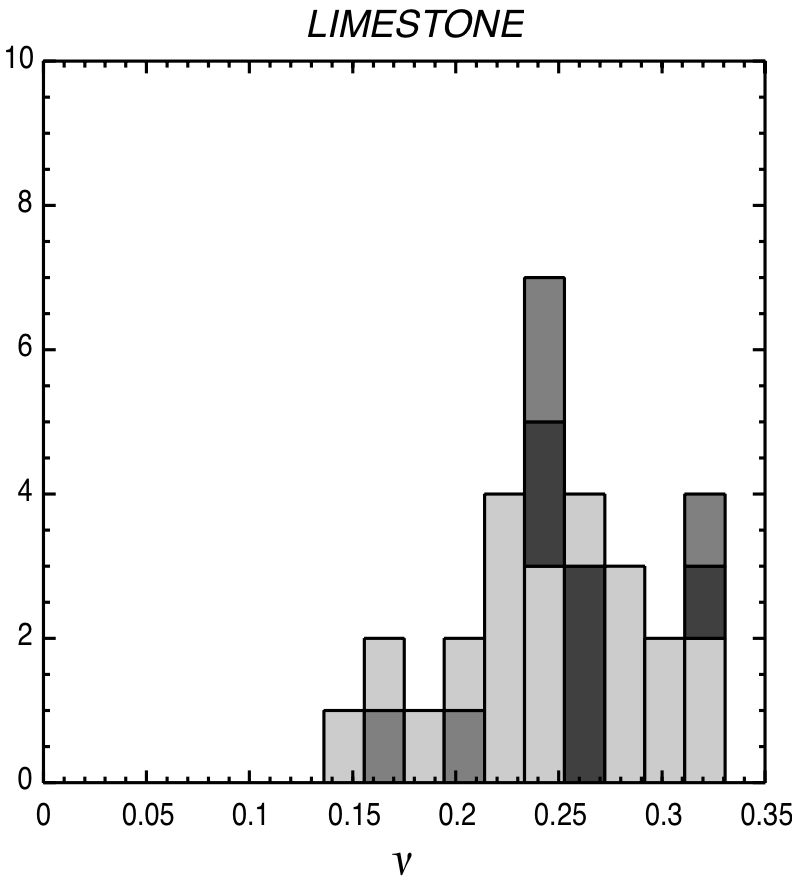
|
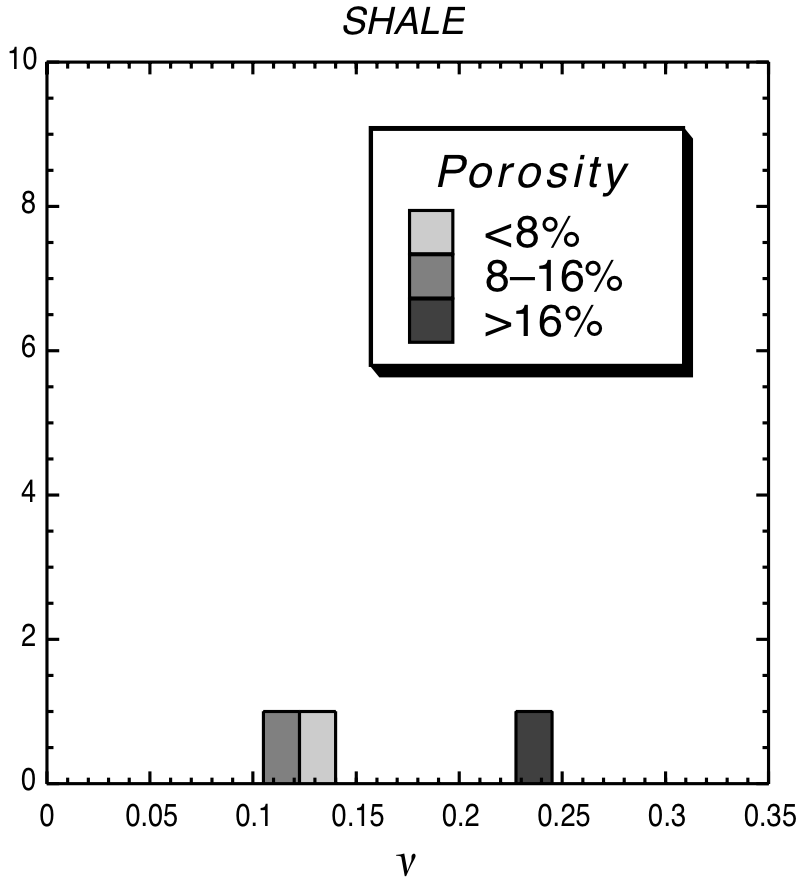
|
© Lama, R. D., and V. S. Vutukuri. HANDBOOK ON MECHANICAL PROPERTIES OF ROCKS-TESTING TECHNIQUES AND RESULTS. VOLUME 2. Monograph. 1978.)
Generalized Hooke’s law
\[\boldsymbol{\sigma} = \mathbb{C} \, \boldsymbol{\varepsilon}\]
For isotropic materials
\[\begin{equation} \small \left\lbrace\begin{matrix} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{12} \\ \sigma_{13} \\ \sigma_{23} \end{matrix}\right\rbrace = \frac{E}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 - \nu & \nu & \nu & 0 & 0 & 0 \\ \nu & 1 - \nu & \nu & 0 & 0 & 0 \\ \nu & \nu & 1 - \nu & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2}(1 - 2 \nu) \end{bmatrix} \left\lbrace\begin{matrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{33} \\ 2\varepsilon_{12} \\ 2\varepsilon_{13} \\ 2\varepsilon_{23} \end{matrix}\right\rbrace \end{equation}\]
\[\mathbf{S} = K \varepsilon_{vol} \mathbf{I} + 2 G \left(\boldsymbol{\varepsilon} - \frac{1}{3} \varepsilon_{vol}\mathbf{I}\right)\]
\[G = \frac{E}{2(1+\nu)} \Rightarrow \mbox{shear modulus}\]
\[\mathbf{S} = \lambda \varepsilon_{vol} \mathbf{I} + 2 G \boldsymbol{\varepsilon} \]
\[\lambda = K - \frac{2}{3} G \Rightarrow \text{Lamé's constant}\]
Relationships between constants
| \(K=\,\) | \(E=\,\) | \(\lambda=\,\) | \(G=\,\) | \(\nu=\,\) | \(M=\,\) | |
| \((K,\,E)\) | \(K\) | \(E\) | \(\tfrac{3K(3K-E)}{9K-E}\) | \(\tfrac{3KE}{9K-E}\) | \(\tfrac{3K-E}{6K}\) | \(\tfrac{3K(3K+E)}{9K-E}\) |
| \((K,\,\lambda)\) | \(K\) | \(\tfrac{9K(K-\lambda)}{3K-\lambda}\) | \(\lambda\) | \(\tfrac{3(K-\lambda)}{2}\) | \(\tfrac{\lambda}{3K-\lambda}\) | \(3K-2\lambda\,\) |
| \((K,\,G)\) | \(K\) | \(\tfrac{9KG}{3K+G}\) | \(K-\tfrac{2G}{3}\) | \(G\) | \(\tfrac{3K-2G}{2(3K+G)}\) | \(K+\tfrac{4G}{3}\) |
| \((K,\,\nu)\) | \(K\) | \(3K(1-2\nu)\,\) | \(\tfrac{3K\nu}{1+\nu}\) | \(\tfrac{3K(1-2\nu)}{2(1+\nu)}\) | \(\nu\) | \(\tfrac{3K(1-\nu)}{1+\nu}\) |
| \((K,\,M)\) | \(K\) | \(\tfrac{9K(M-K)}{3K+M}\) | \(\tfrac{3K-M}{2}\) | \(\tfrac{3(M-K)}{4}\) | \(\tfrac{3K-M}{3K+M}\) | \(M\) |
| \((E,\,\lambda)\) | \(\tfrac{E + 3\lambda + R}{6}\) | \(E\) | \(\lambda\) | \(\tfrac{E-3\lambda+R}{4}\) | \(\tfrac{2\lambda}{E+\lambda+R}\) | \(\tfrac{E-\lambda+R}{2}\) |
| \((E,\,G)\) | \(\tfrac{EG}{3(3G-E)}\) | \(E\) | \(\tfrac{G(E-2G)}{3G-E}\) | \(G\) | \(\tfrac{E}{2G}-1\) | \(\tfrac{G(4G-E)}{3G-E}\) |
| \((E,\,\nu)\) | \(\tfrac{E}{3(1-2\nu)}\) | \(E\) | \(\tfrac{E\nu}{(1+\nu)(1-2\nu)}\) | \(\tfrac{E}{2(1+\nu)}\) | \(\nu\) | \(\tfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}\) |
| \((E,\,M)\) | \(\tfrac{3M-E+S}{6}\) | \(E\) | \(\tfrac{M-E+S}{4}\) | \(\tfrac{3M+E-S}{8}\) | \(\tfrac{E-M+S}{4M}\) | \(M\) |
| \((\lambda,\,G)\) | \(\lambda+ \tfrac{2G}{3}\) | \(\tfrac{G(3\lambda + 2G)}{\lambda + G}\) | \(\lambda\) | \(G\) | \(\tfrac{\lambda}{2(\lambda + G)}\) | \(\lambda+2G\,\) |
| \((\lambda,\,\nu)\) | \(\tfrac{\lambda(1+\nu)}{3\nu}\) | \(\tfrac{\lambda(1+\nu)(1-2\nu)}{\nu}\) | \(\lambda\) | \(\tfrac{\lambda(1-2\nu)}{2\nu}\) | \(\nu\) | \(\tfrac{\lambda(1-\nu)}{\nu}\) |
| \((\lambda,\,M)\) | \(\tfrac{M + 2\lambda}{3}\) | \(\tfrac{(M-\lambda)(M+2\lambda)}{M+\lambda}\) | \(\lambda\) | \(\tfrac{M-\lambda}{2}\) | \(\tfrac{\lambda}{M+\lambda}\) | \(M\) |
| \((G,\,\nu)\) | \(\tfrac{2G(1+\nu)}{3(1-2\nu)}\) | \(2G(1+\nu)\,\) | \(\tfrac{2 G \nu}{1-2\nu}\) | \(G\) | \(\nu\) | \(\tfrac{2G(1-\nu)}{1-2\nu}\) |
| \((G,\,M)\) | \(M - \tfrac{4G}{3}\) | \(\tfrac{G(3M-4G)}{M-G}\) | \(M - 2G\,\) | \(G\) | \(\tfrac{M - 2G}{2M - 2G}\) | \(M\) |
| \((\nu,\,M)\) | \(\tfrac{M(1+\nu)}{3(1-\nu)}\) | \(\tfrac{M(1+\nu)(1-2\nu)}{1-\nu}\) | \(\tfrac{M \nu}{1-\nu}\) | \(\tfrac{M(1-2\nu)}{2(1-\nu)}\) | \(\nu\) | \(M\) |
Siesmic wave velocity
\[V_p = \sqrt{\frac{M}{\rho}}, \quad \quad V_s = \sqrt{\frac{G}{\rho}}\]
Shortcourse on Reservoir Geomechanics - John T. Foster - May 2023