Stress

Recall: stress tensor

\[ \mathbf{S} = \begin{bmatrix} S_{11} & S_{12} & S_{13} \\ S_{21} & S_{22} & S_{23} \\ S_{31} & S_{32} & S_{33} \end{bmatrix} \]

Due to conservation of angular momentum: \(S_{12} = S_{21}, S_{13} = S_{31}\) and \(S_{32} = S_{23}\) .

\[ \mathbf{S} = \begin{bmatrix} S_{11} & S_{12} & S_{13} \\ S_{12} & S_{22} & S_{23} \\ S_{13} & S_{23} & S_{33} \end{bmatrix} \]

Principle stresses and directions

\[\mathbf{S}' = \mathbf{Q}^{-1} \mathbf{S Q}\]

\[ \mathbf{S}' = \begin{bmatrix} S_1 & 0 & 0 \\ 0 & S_2 & 0 \\ 0 & 0 & S_3 \end{bmatrix} \]

with \(S_1 \gt S_2 \gt S_3\) where the \(S_i\)’s are the eigenvalues of \(\mathbf{S}\)

\[ \mathbf{Q} = [ \vec{v}_1 \; \vert \; \vec{v}_2 \; \vert \; \vec{v}_3 ] \]

where \(\vec{v}_1\) is the eigenvector corresponding to \(S_1\), \(\vec{v}_2\) is the eigenvector corresponding to \(S_2\), and \(\vec{v}_3\) is the eigenvector corresponding to \(S_3\).

Example

Determine the principle stresses and directions given:

\[ \mathbf{S} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & -1 \\ 0 & -1 & 3 \end{bmatrix} \]

\[ S_1 = 4, \quad S_2 = 2, \quad S_3 = 1 \]

\[ \mathbf{Q} = [ \vec{v}_1 \; \vert \; \vec{v}_2 \; \vert \; \vec{v}_3 ] = \begin{bmatrix} 0 & 0 & 1 \\ -1 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix} \]

Conservation of linear momentum

\[\begin{align} \rho \frac{\partial^2 u_1}{\partial t^2} &= \frac{\partial S_{11}}{\partial x_1} + \frac{\partial S_{12}}{\partial x_2} + \frac{\partial S_{13}}{\partial x_3} + \rho b_1 \\ \rho \frac{\partial^2 u_2}{\partial t^2} &= \frac{\partial S_{12}}{\partial x_1} + \frac{\partial S_{22}}{\partial x_2} + \frac{\partial S_{23}}{\partial x_3} + \rho b_2 \\ \rho \frac{\partial^2 u_1}{\partial t^2} &= \frac{\partial S_{13}}{\partial x_1} + \frac{\partial S_{23}}{\partial x_2} + \frac{\partial S_{33}}{\partial x_3} + \rho b_3 \end{align}\]

Principle stresses and directions in the earth

Idealized half-space

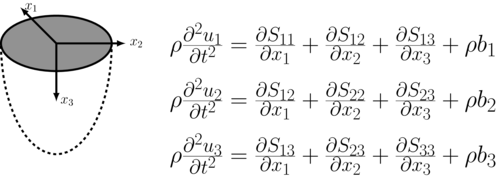
\(S_{33} = S_v\) must be a principle stress!

Four parameters needed to describe state-of-stress in the earth

• \(S_\mbox{v}\) - vertical stress magnitude
• \(S_{\mbox{Hmax}}\) - maximum horizontal principle stress magnitude
• \(S_\mbox{hmin}\) - minimum horizontal principle stress magnitude
• One horizontal principle direction, usually the direction associated with \(S_\mbox{Hmax}\)