Effective stress

Effective stress tensor

\[ \boldsymbol{\sigma}_{eff} = \begin{bmatrix} S_{11} & S_{12} & S_{13} \\ S_{12} & S_{22} & S_{23} \\ S_{13} & S_{23} & S_{33} \end{bmatrix} - \begin{bmatrix} P_p & 0 & 0 \\ 0 & P_p & 0 \\ 0 & 0 & P_p \end{bmatrix} \]

\[ \boldsymbol{\sigma}_{eff}= \begin{bmatrix} S_{11} - P_p & S_{12} & S_{13} \\ S_{12} & S_{22} - P_p & S_{23} \\ S_{13} & S_{23} & S_{33} - P_p \end{bmatrix} \]

• Faulting depends on the effective stress

Stress magnitudes at depth

Normal faulting

Hydrostatic

Overpressure

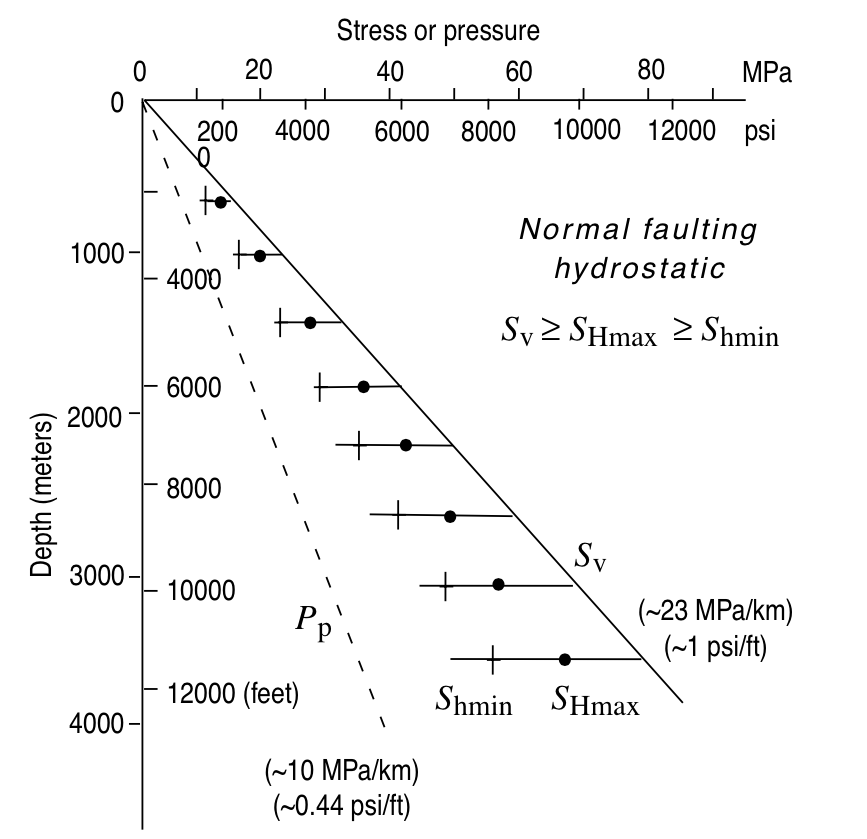
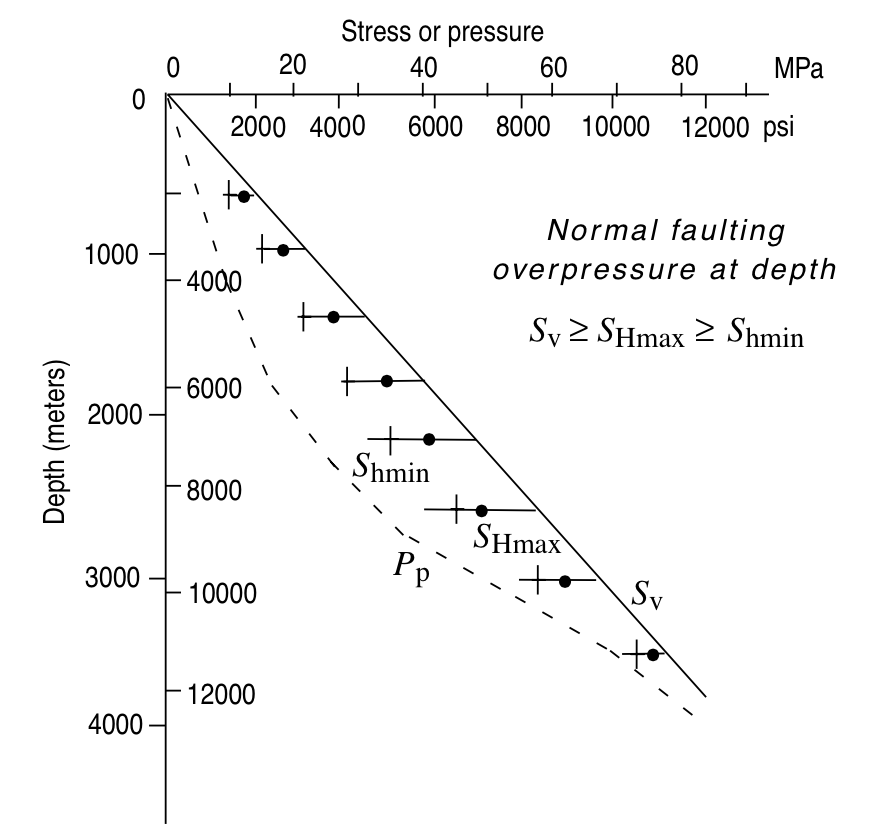
© Cambridge University Press Zoback (Fig. 1.4, pp. 13)

These suggestive figures are established by 1) Anderson faulting theory (which defines the relative stress magnitude), (ii) the fact that the least principal stress must always exceed the pore pressure (to avoid hydraulic fracturing), and (iii) the difference between the minimum and maximum principal stress which cannot exceed the strength of the crust (which depends on depth and pore pressure.

Strike-slip faulting

Hydrostatic

Overpressure

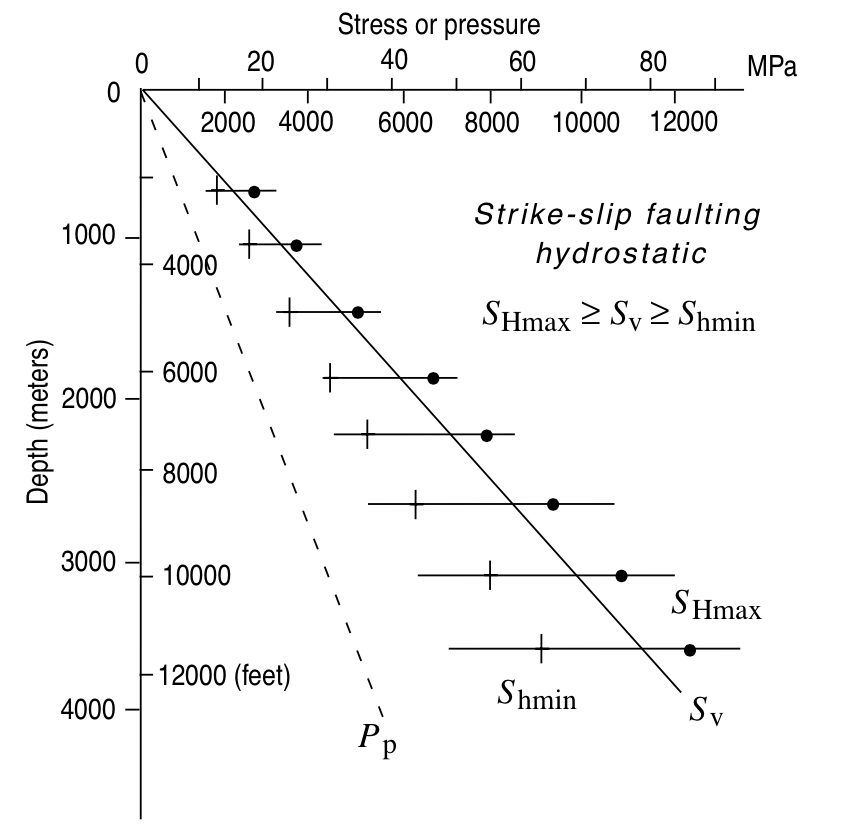
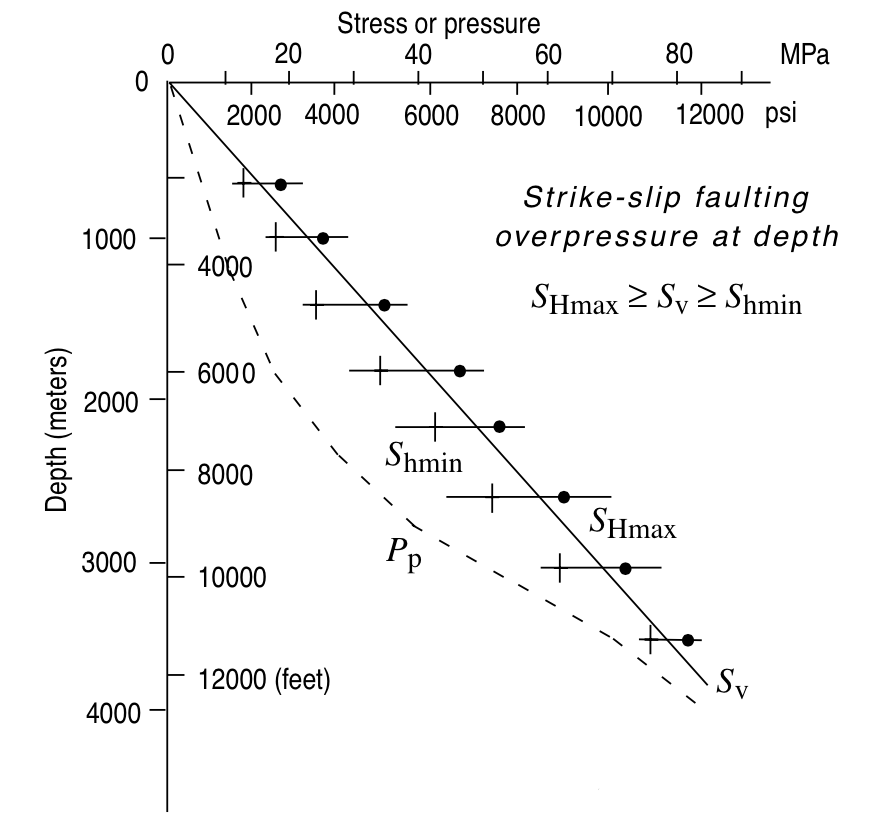
© Cambridge University Press Zoback (Fig. 1.4, pp. 13)

Reverse faulting

Hydrostatic

Overpressure

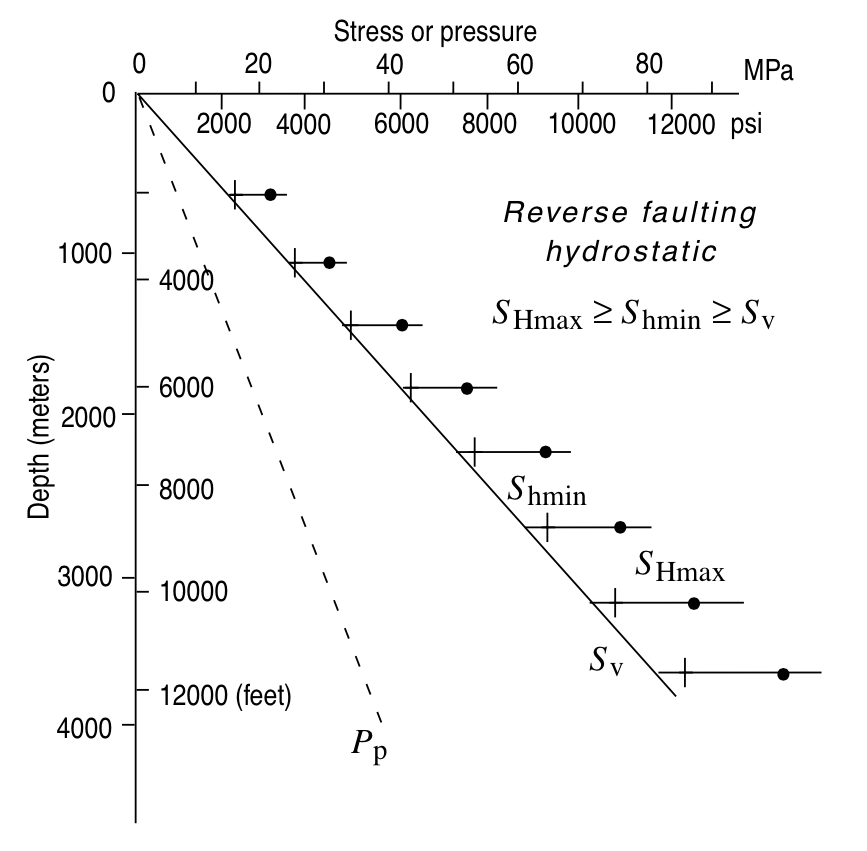
© Cambridge University Press Zoback (Fig. 1.4, pp. 13)

Stress measurement techniques

• \(S_v\) - integration of density logs

• \(S_{3}\) (\(S_{hmin}\), except in reverse faulting) is obtained from mini-fracs and leak-off tests. Zoback (Chapter 6)

• \(P_p\) measure directly or estimated from geophysical logs or siesmic data. Zoback (Chapter 2)

• Bound \(S_{Hmax}\) with frictional strength of crust or oberservations of wellbore failures. Zoback (Chapter 4, 7, 8)

• Orientation of principal stresses from wellbore observations, geology, earthquake focal mechanisms. Zoback (Chapter 5, 6)

Stress maps

Heidbach, O., Tingay, M., Barth, A., Reinecker, J., Kurfeß, D., and Müller, B., The World Stress Map database release 2008 DOI:10.1594/GFZ.WSM.Rel2008, 2008

Pore pressure at depth

\(P_p^{\mbox{hydro}} = \int_0^z \rho_w(z) g {\rm d}z \approx \rho_w g z_w\)

Ratio of pore pressure to \(S_v\)

\(\lambda_p = P_p / S_v\)

Hydrostatic: \(\lambda_p \approx 0.44\)

Lithostatic: \(\lambda_p = 1\)

Overpressure

Monte Cristo field (onshore near Gulf of Mexico, Texas)

© Cambridge University Press Zoback (Fig. 2.2, pp. 30)

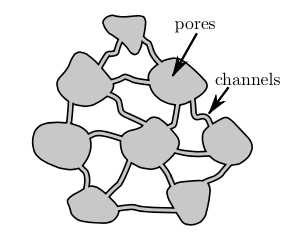
Hydrostatic is characterized by uniform and connected pores.

Reservior Compartmentalization

© Cambridge University Press Zoback (Fig. 2.4, pp. 32)