Multi-Output Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Uncertainties

Mingyuan Yang
mingyuanyang@pku.edu.cn

Peking University

The University of Texas at Austin

John T. Foster
john.foster@utexas.edu

Hildebrand Department of Petroleum and Geosystems Engineering

Department of Aerospace Engineering and Engineering Mechanics

Oden Institute for Computational Engineering and Science

The University of Texas at Austin

August 18, 2023

Physics Informed Neural Networks

PINNs

Introduced in (Raissi, Perdikaris, and Karniadakis 2019) as a general method for solving partial differential equations.

Already recieved >5900 citations since posting on arXiv in 2018!

Generic PINN architecture

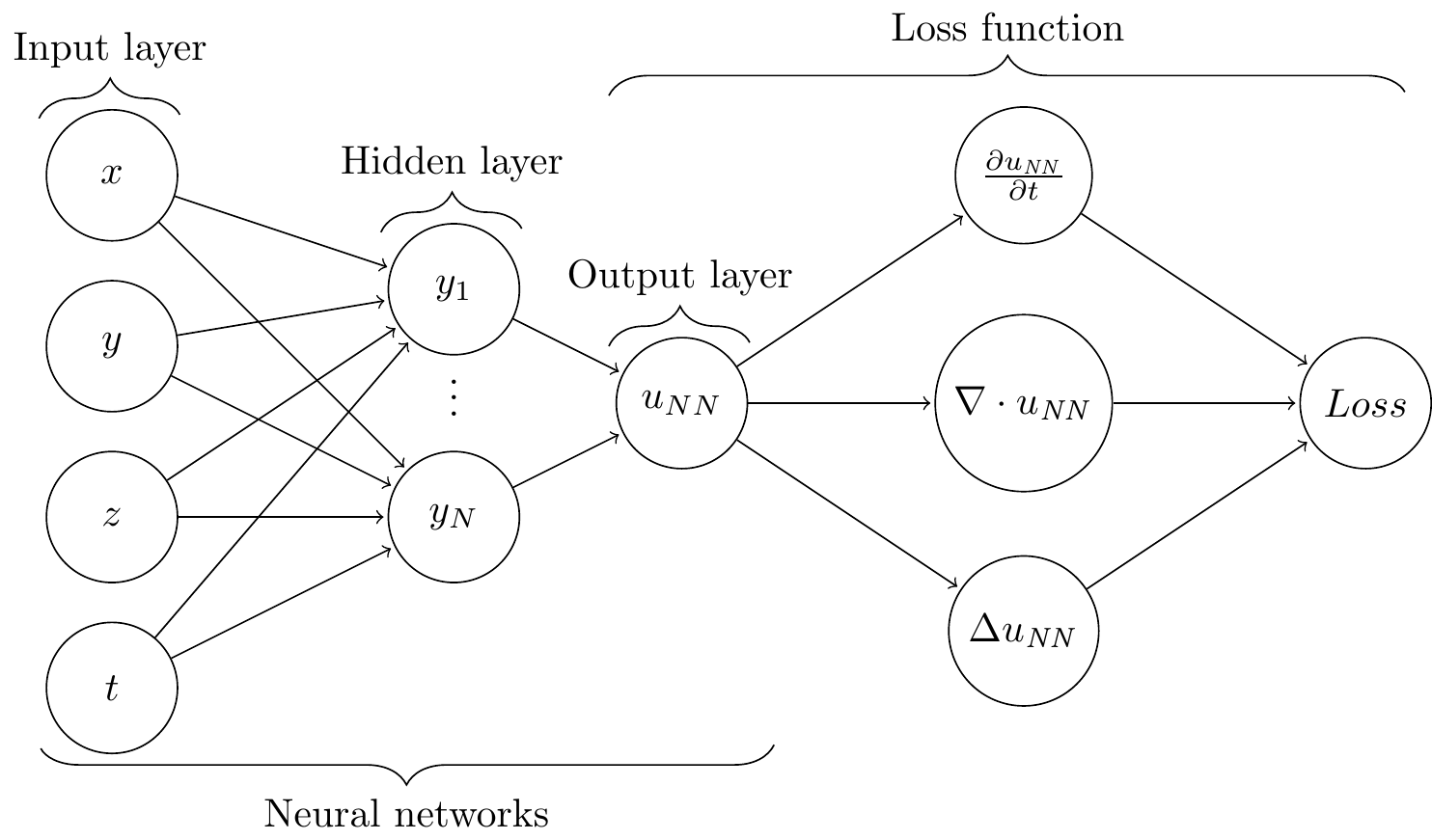
Loss function for generic PINN system

\[ \begin{align} r_d(u_{NN}, f_{NN}) &= \mathcal{L} u_{NN} - f_{NN},\qquad x \in \Omega \\ r_e(u_{NN}) &= u_{NN} - h,\qquad x \in \partial \Omega_h \\ r_n(u_{NN}) &= \frac{\partial u_{NN}}{\partial x} - g,\qquad x \in \partial \Omega_g \\ r_{u}(u_{NN}) &= u_{NN}(x^u_i) - u_m(x^u_i), \qquad i=1,2,...,n \\ r_{f}(f_{NN}) &= f_{NN}(x^f_i) - f_m(x^f_i), \qquad i=1,2,...,m \end{align} \]

\[ \begin{gather} L_{MSE} = \frac{1}{N}\sum_{i}^N r_d^2 + \frac{1}{N_e}\sum_{i=1}^{N_e} r_e^2 + \frac{1}{N_n}\sum_{i=1}^{N_n} r_n^2 + \frac{1}{n}\sum_{i=1}^{n} r_{u}^2 + \frac{1}{m}\sum_{i=1}^m r_{f}^2 \end{gather} \]

Extensions of PINNs for UQ

Multi-Output PINN

MO-PINN (M. Yang and Foster 2022)

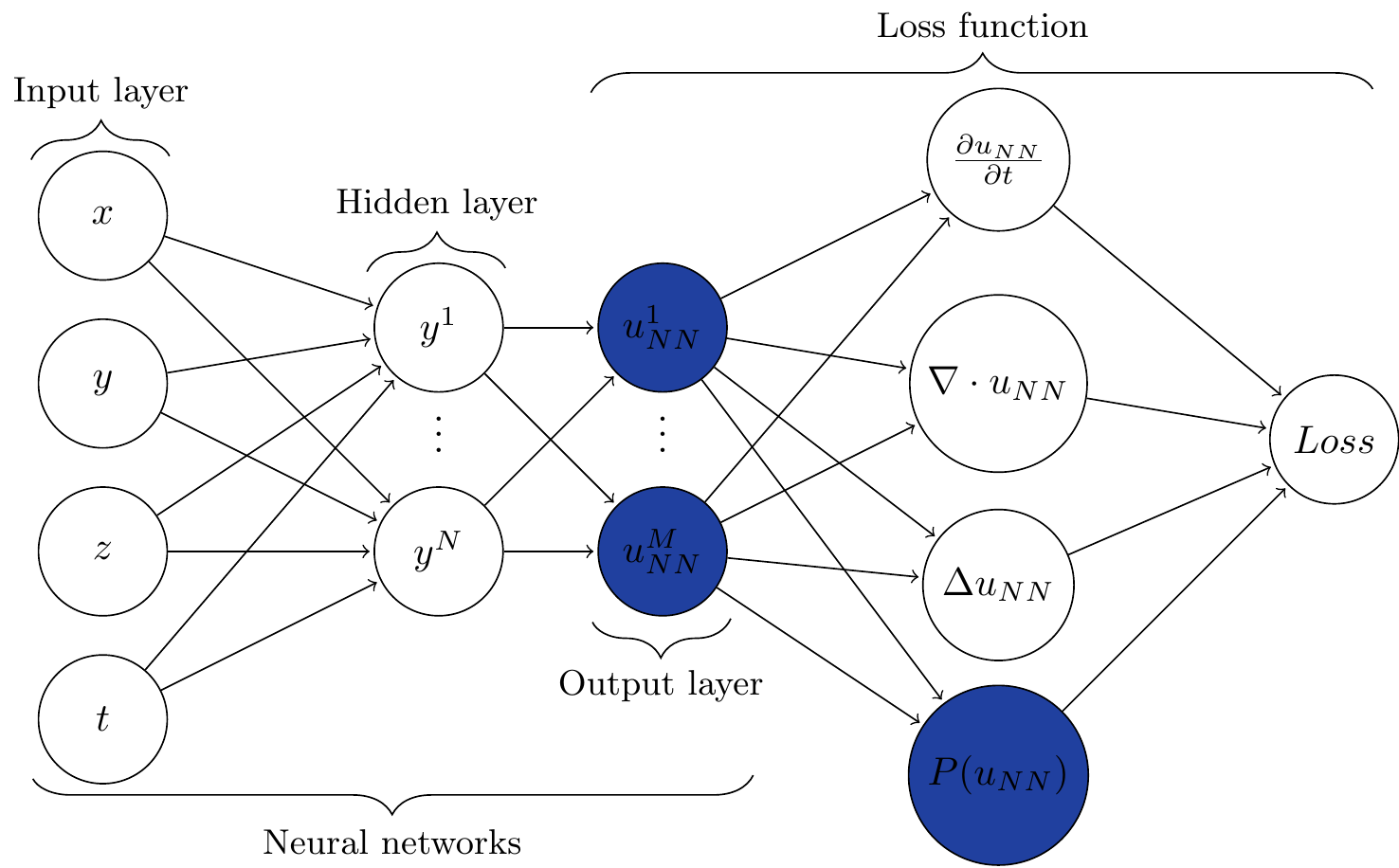
Loss function for generic MO-PINN system

\[ \begin{align} r_d(u_{NN}^j, f_{NN}^j) &= \mathcal{L} u_{NN}^j - f_{NN}^j,\qquad x \in \Omega \\ r_e(u_{NN}^j) &= u_{NN}^j - h,\qquad x \in \partial \Omega_h \\ r_n(u_{NN}^j) &= \frac{\partial u_{NN}^j}{\partial x} - g,\qquad x \in \partial \Omega_g \\ r_{um}(u_{NN}^j) &= u_{NN}^j(x^u_i) - \left(u_m(x^u_i) + \sigma_u^j\right), \qquad i=1,2,...,n \\ r_{fm}(f_{NN}^j) &= f_{NN}^j(x^f_i) - \left(f_m(x^f_i) + \sigma_f^j\right), \qquad i=1,2,...,m \ \end{align} \]

\[ \begin{gather} L_{MSE} = \frac{1}{M}\sum_{j=1}^{M} \left( \frac{1}{N}\sum_{i}^N r_d^2 + \frac{1}{N_e}\sum_{i=1}^{N_e} r_e^2 + \frac{1}{N_n}\sum_{i=1}^{N_n} r_n^2 + \frac{1}{n}\sum_{i=1}^{n} r_{um}^2 + \frac{1}{m}\sum_{i=1}^m r_{fm}^2 \right) \end{gather} \]

Forward PDE problems

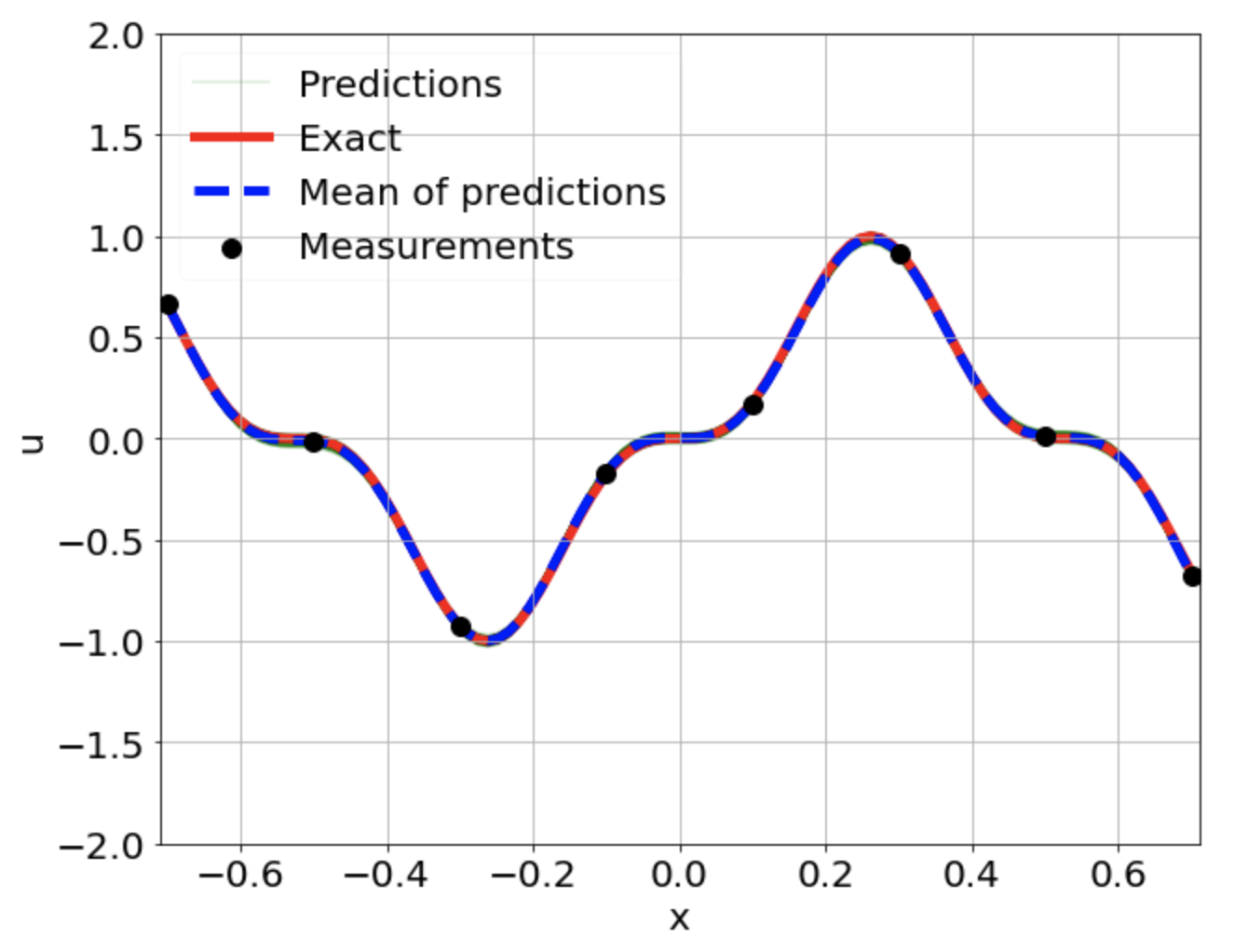
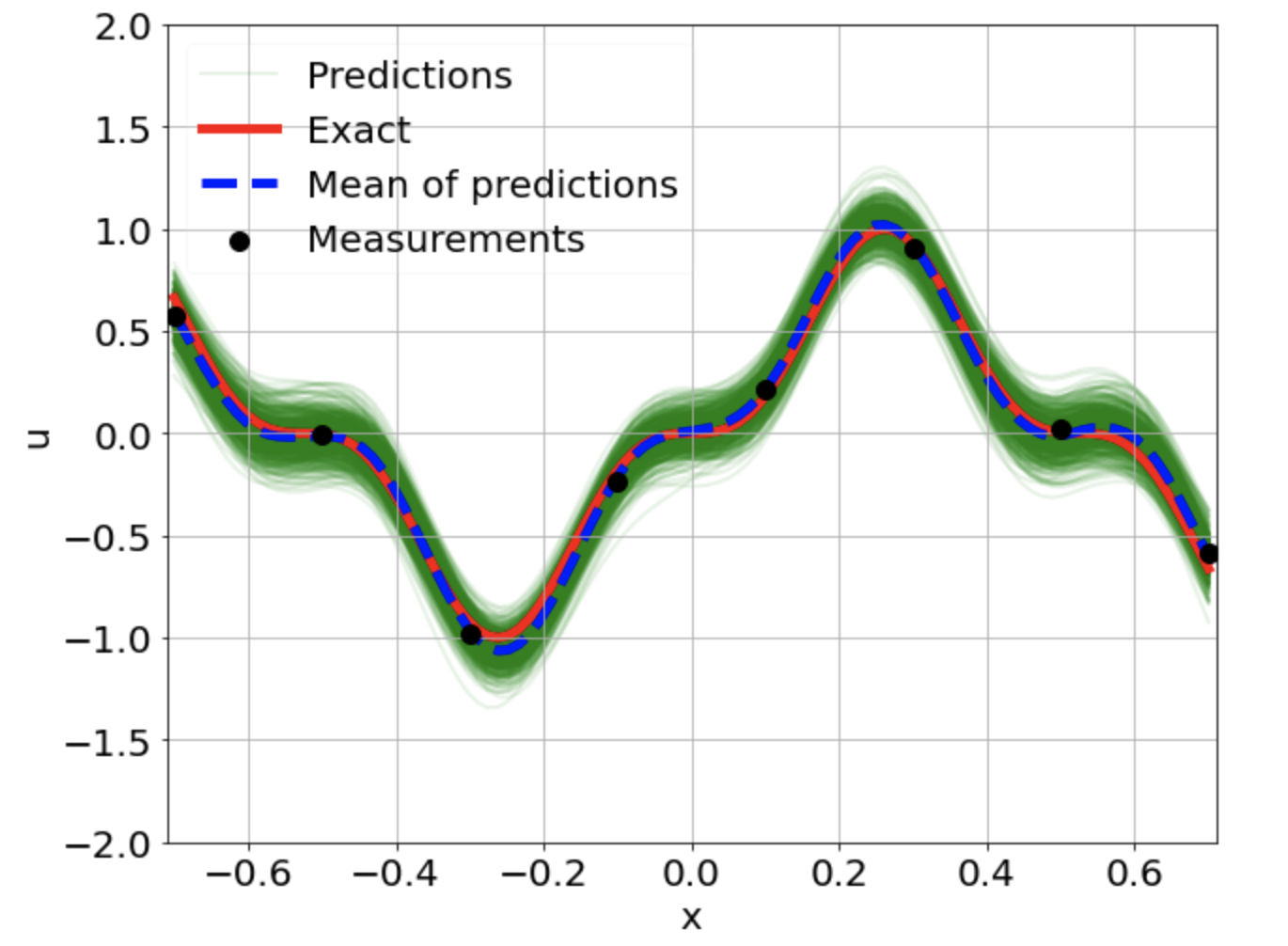
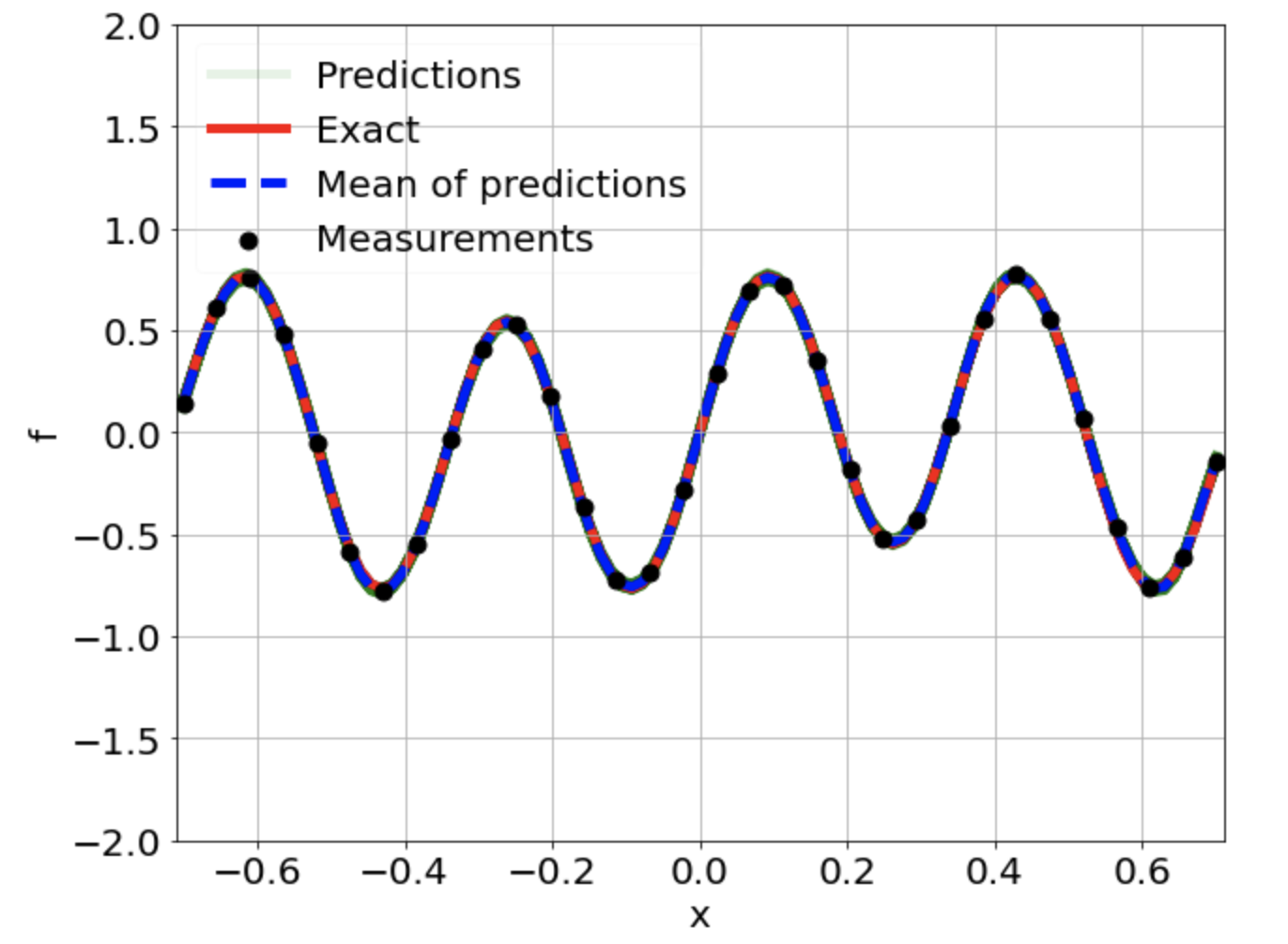
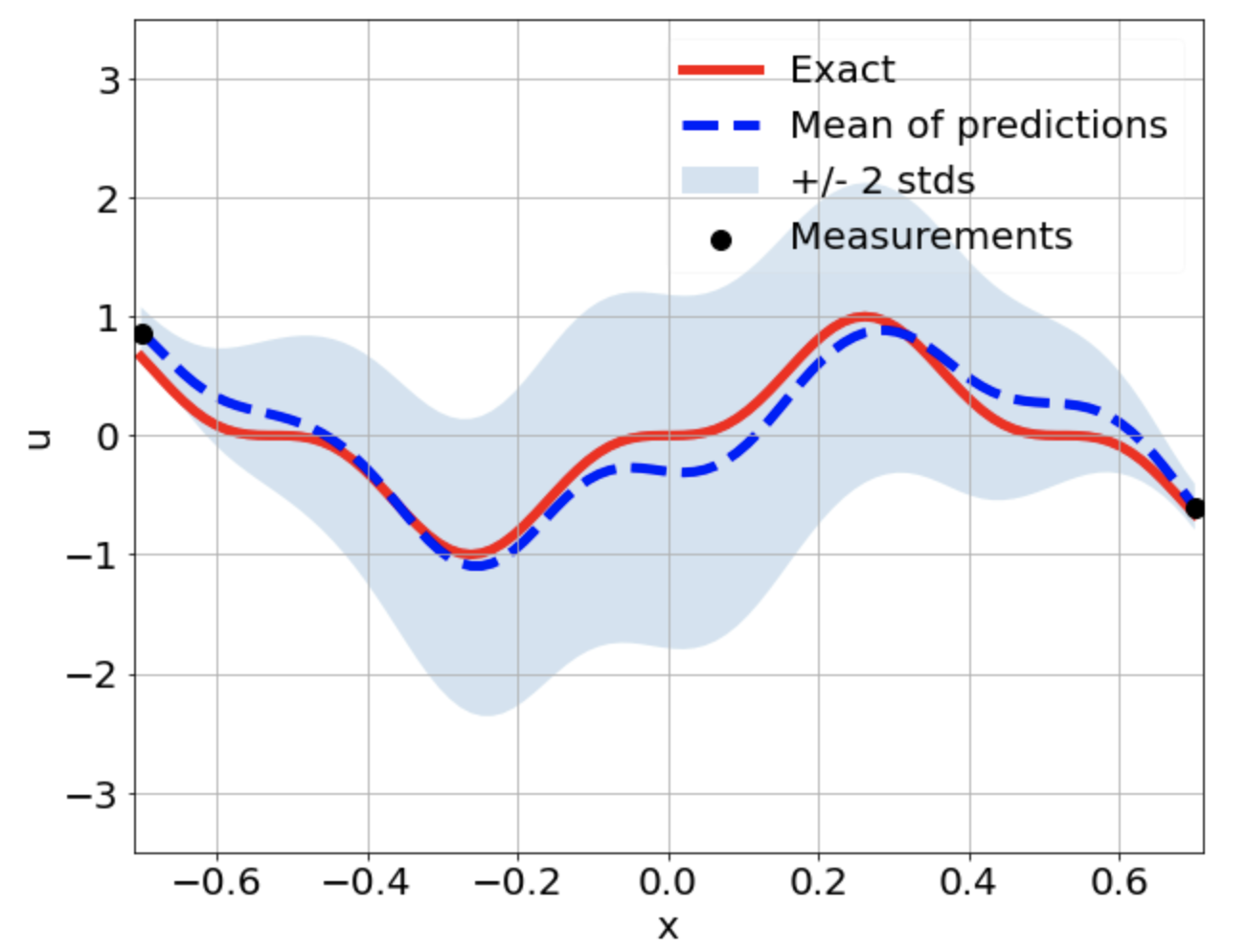
One-dimensional linear Poisson equation

\[ \begin{gathered} \lambda \frac{\partial^2 u}{\partial x^2} = f, \qquad x \in [-0.7, 0.7] \end{gathered} \] where \(\lambda = 0.01\) and \(u=\sin^3(6x)\)

Solution \(u\)

Source \(f\) from manufactured solution

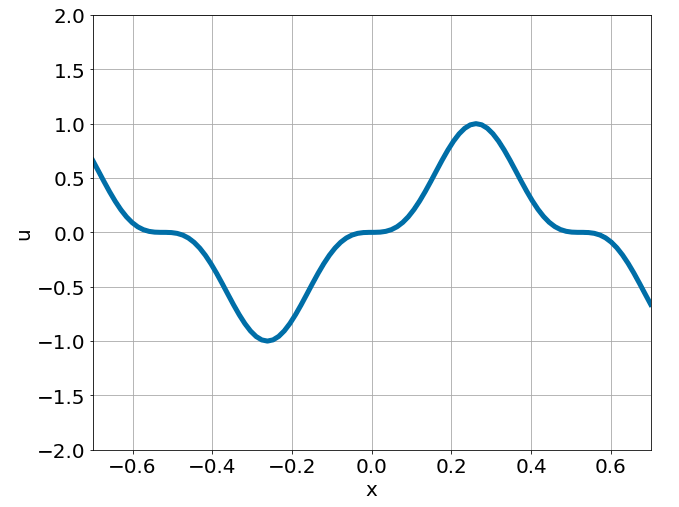
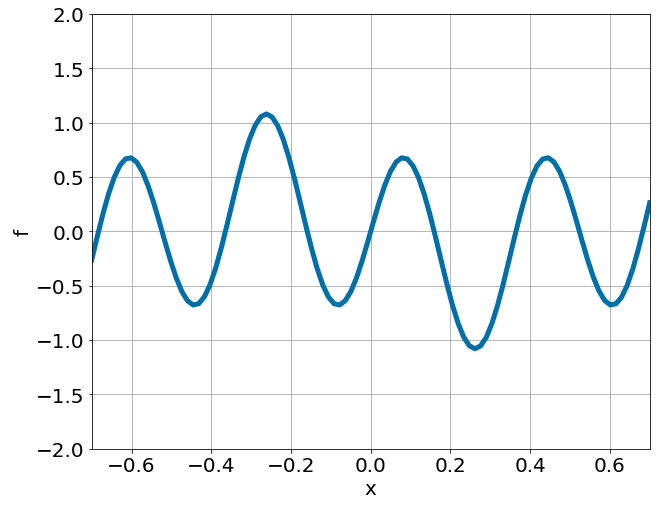
Network architecture and hyperparameters

  • 2 neural networks: \(u_{NN}\) and \(f_{NN}\)

  • 2 hidden layers with 20 and 40 neurons each

  • \(\tanh\) activation function

  • ADAM optimizer

  • \(10^{-3}\) learning rate

  • Xavier normalization

  • 10000 epochs

  • 500 outputs

Predictions w/ \(\sigma = 0.01\) noise on measurements

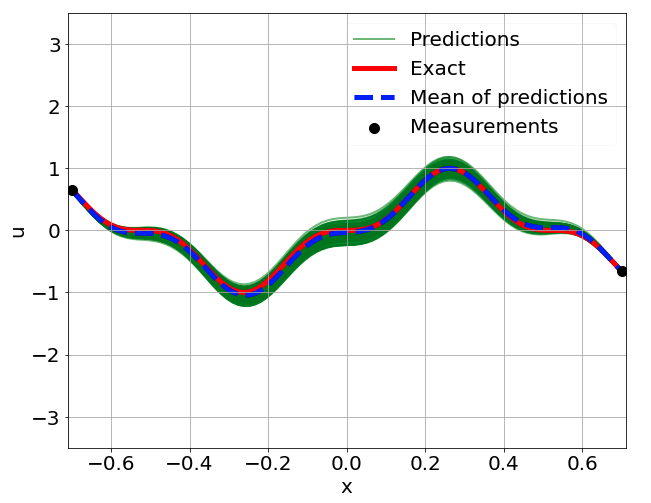
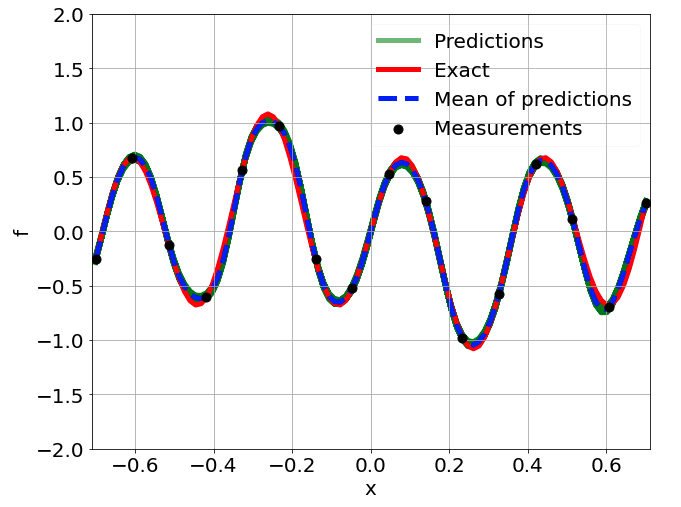
Prediction \(u\) w/ raw solutions

Prediction \(f\) w/ raw solutions

Prediction \(u\) w/ \(2\sigma\) distribution

Prediction \(f\) w/ \(2\sigma\) distribution

Predictions w/ \(\sigma = 0.1\) noise on measurements

Prediction \(u\) w/ raw solutions

Prediction \(f\) w/ raw solutions

Prediction \(u\) w/ \(2\sigma\) distribution

Prediction \(f\) w/ \(2\sigma\) distribution

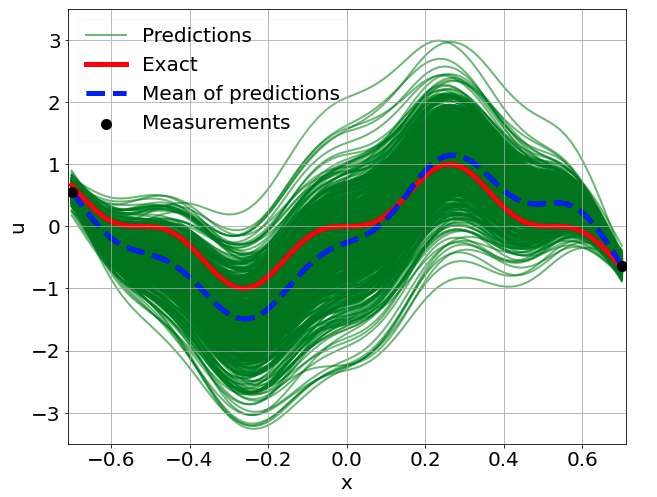
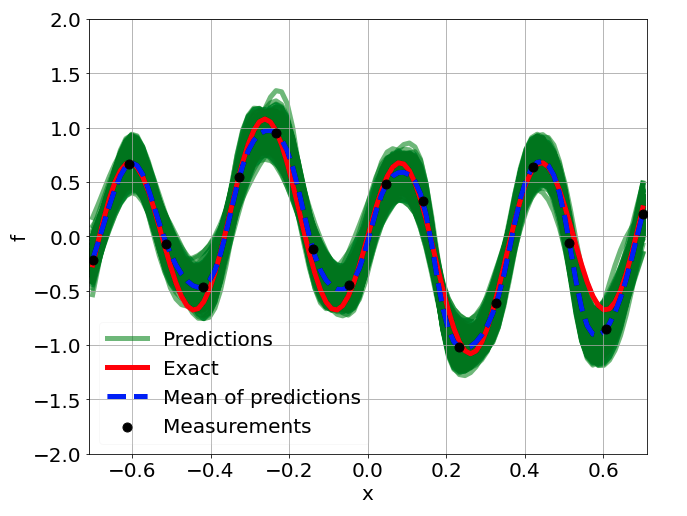
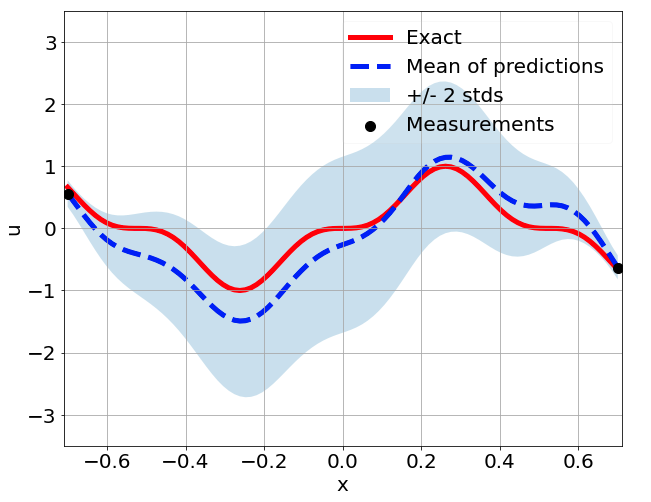
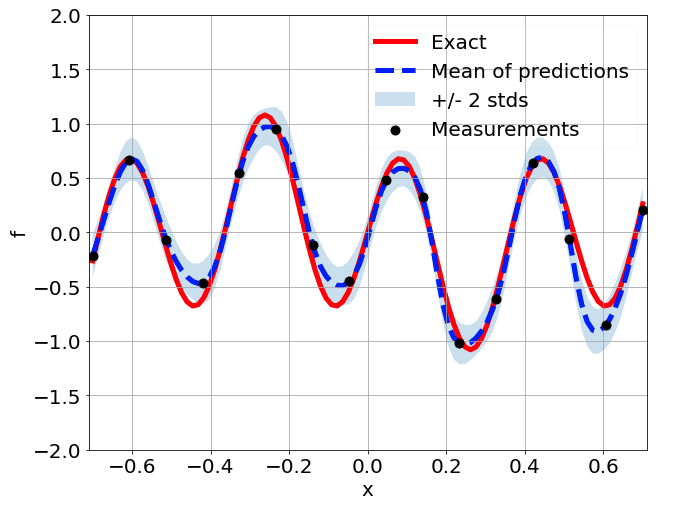
Sensitivity to random network parameter initialization

\(\sigma = 0.1\) noise

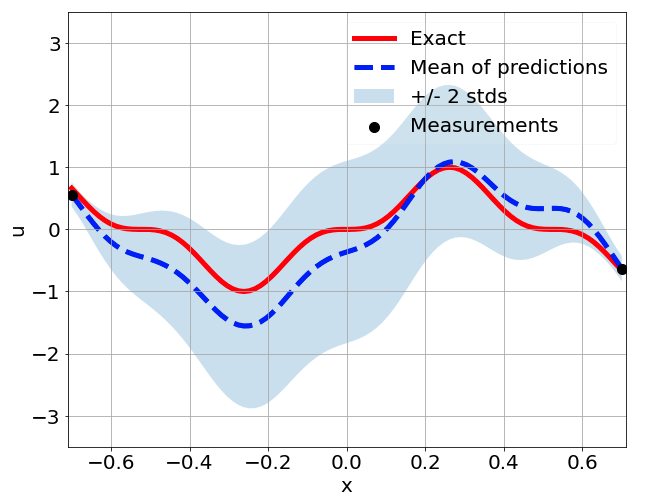
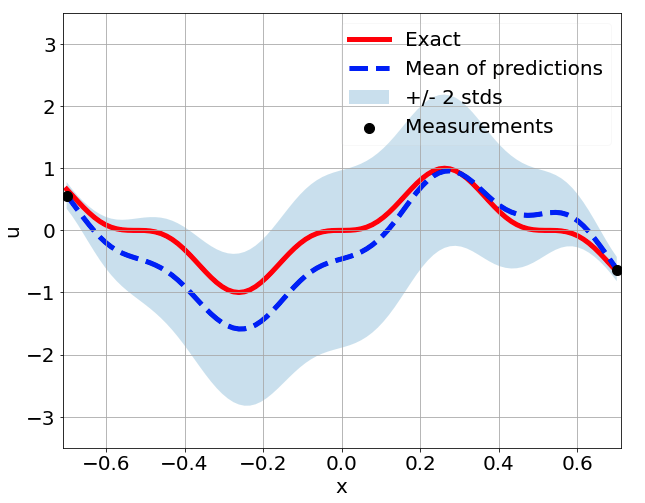
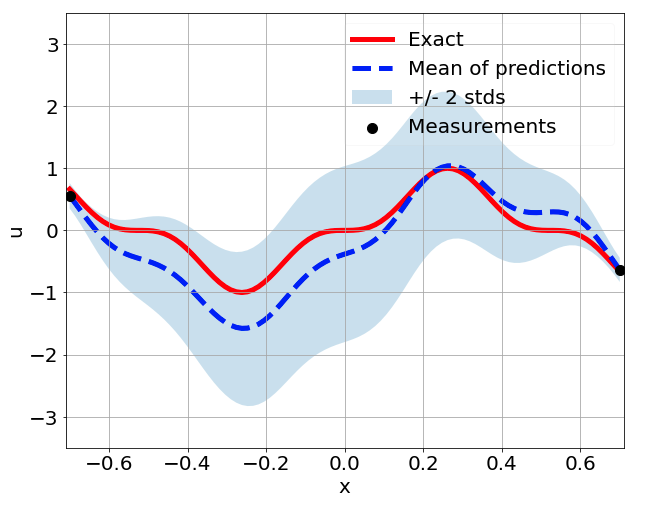
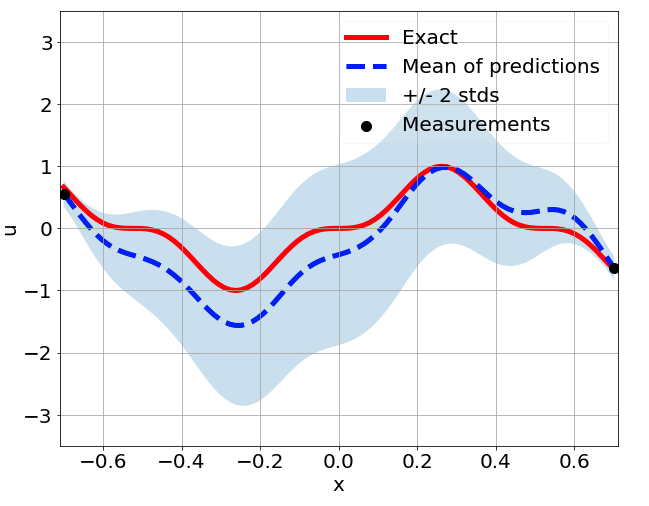
Sensitivity to measurement sampling

\(\sigma = 0.1\) noise

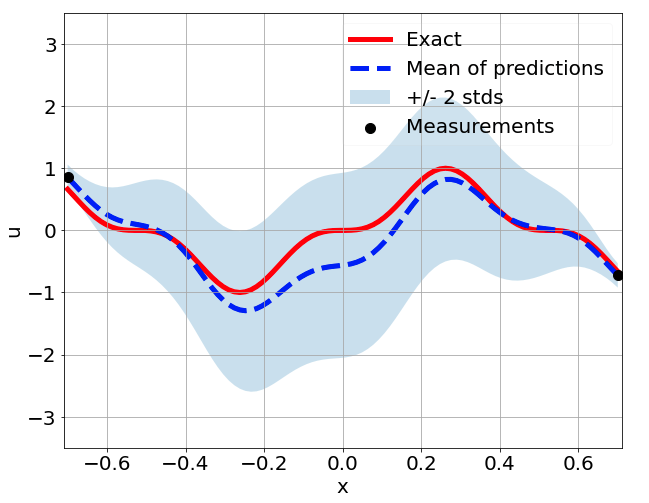
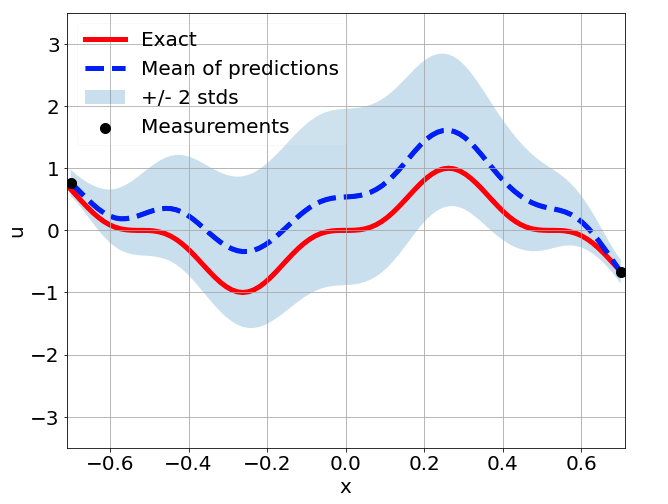
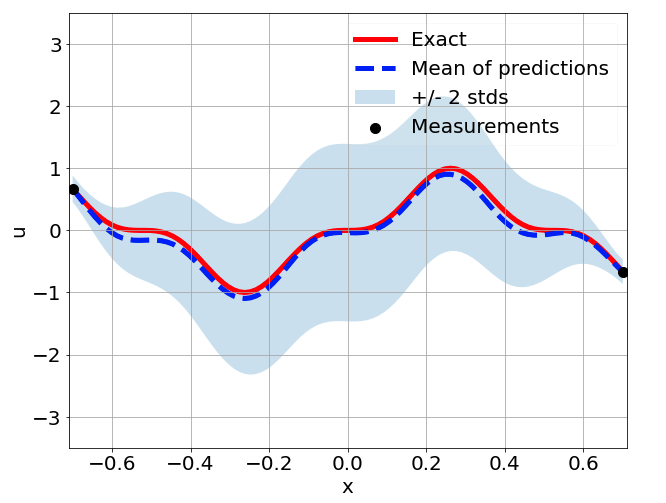
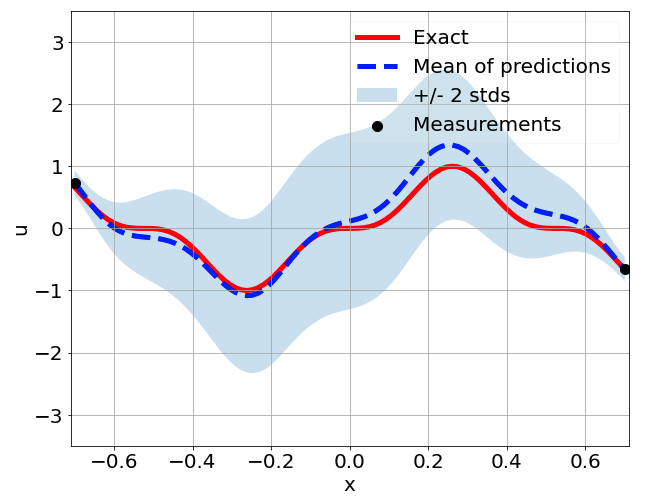
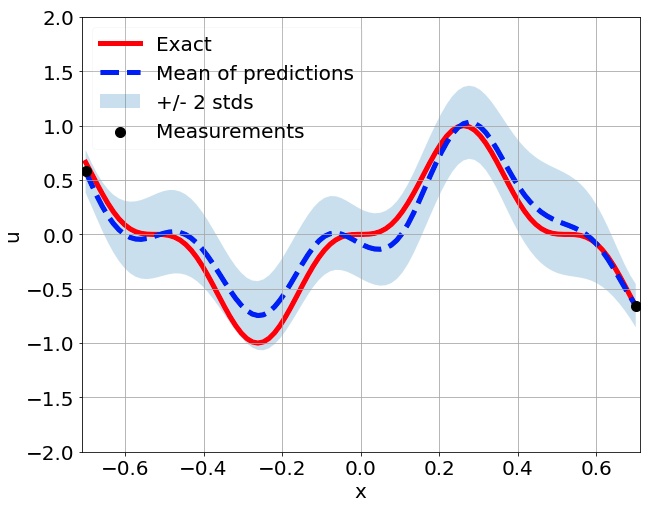
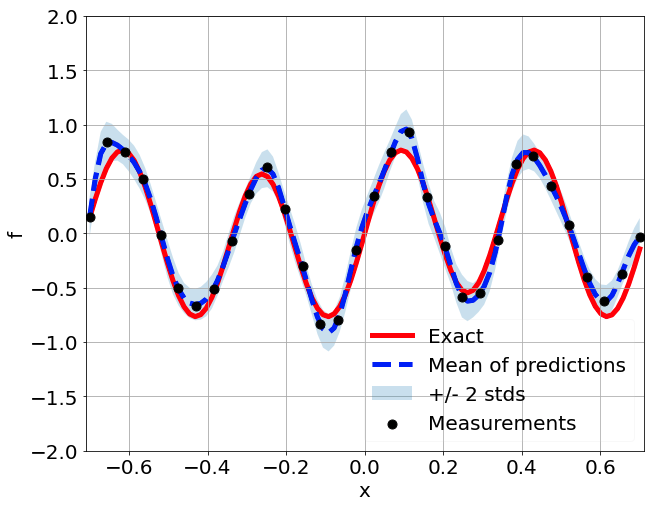
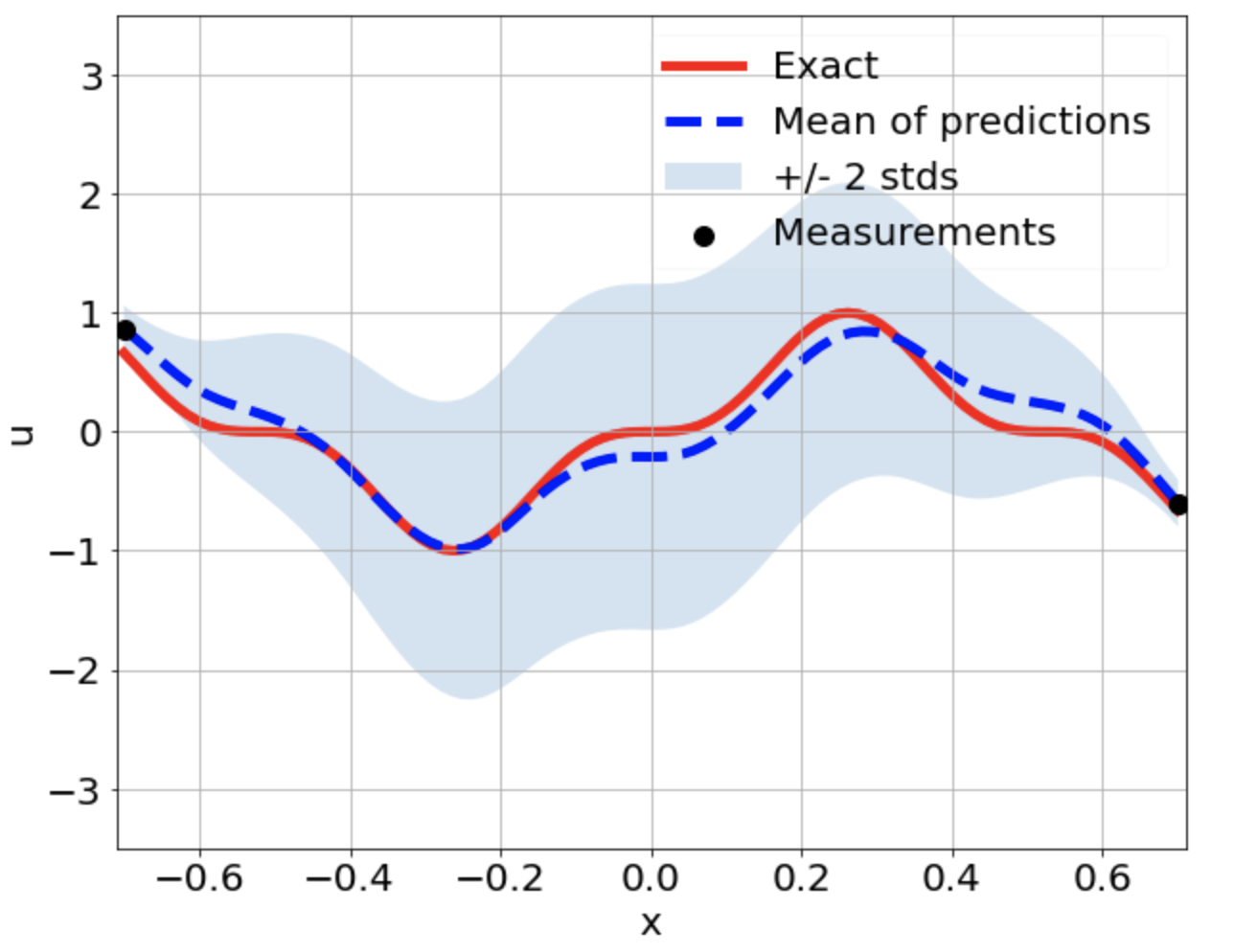
One-dimensional nonlinear Poisson equation

\[ \begin{gathered} \lambda \frac{\partial^2 u}{\partial x^2} + k \tanh(u) = f, \qquad x \in [-0.7, 0.7] \end{gathered} \] where \(\lambda = 0.01, k=0.7\) and \(u=\sin^3(6x)\)

Solution \(u\)

Source \(f\) from manufactured solution

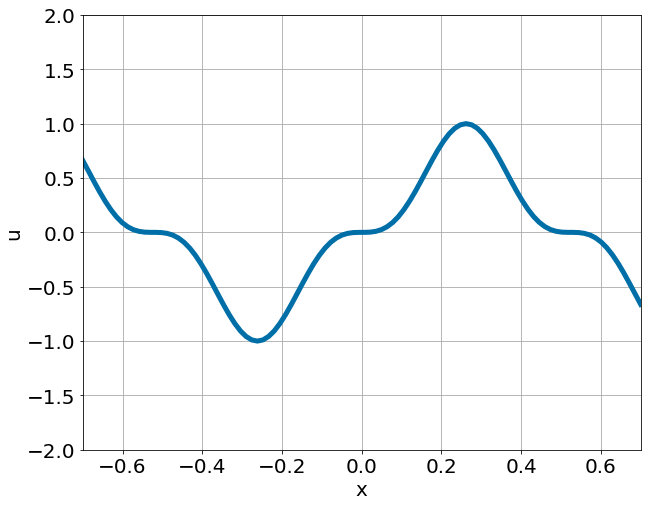
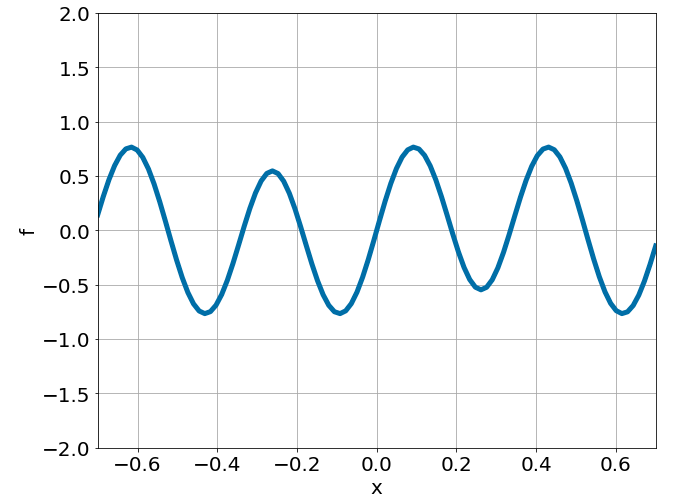
Predictions w/ \(\sigma = 0.01\) noise on measurements

Prediction \(u\) w/ raw solutions

Prediction \(f\) w/ raw solutions

Prediction \(u\) w/ \(2\sigma\) distribution

Prediction \(f\) w/ \(2\sigma\) distribution

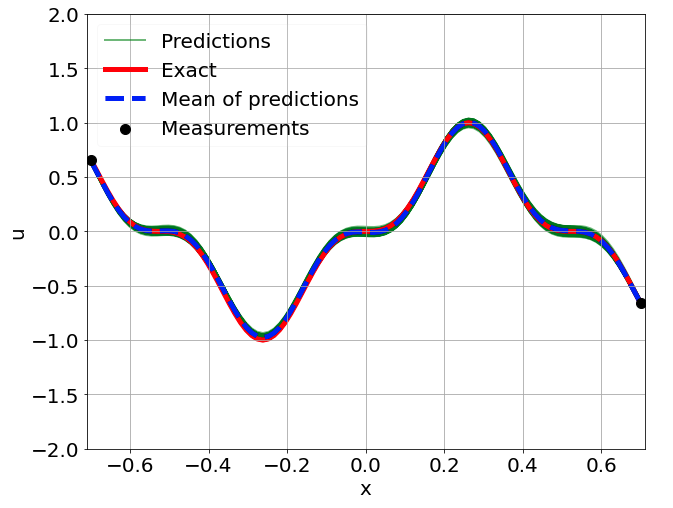
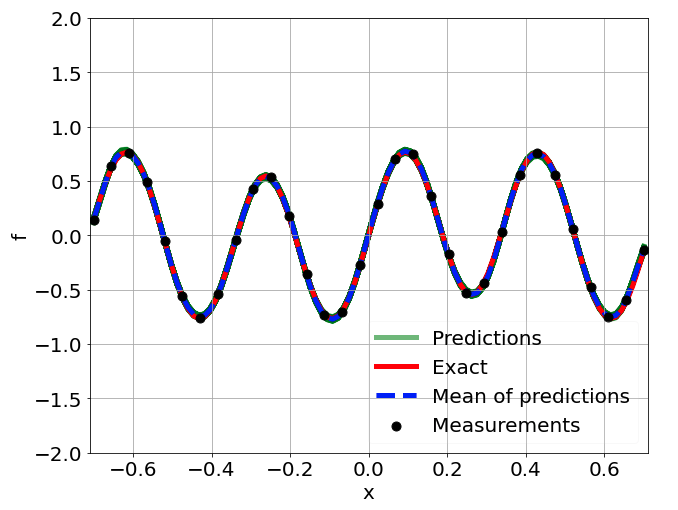
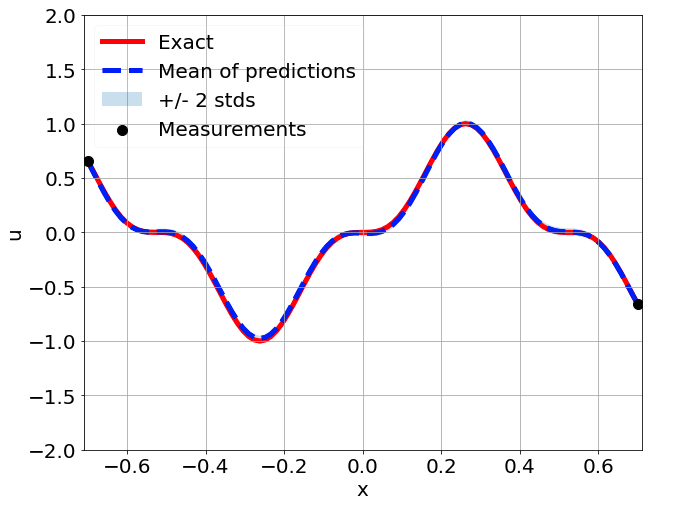
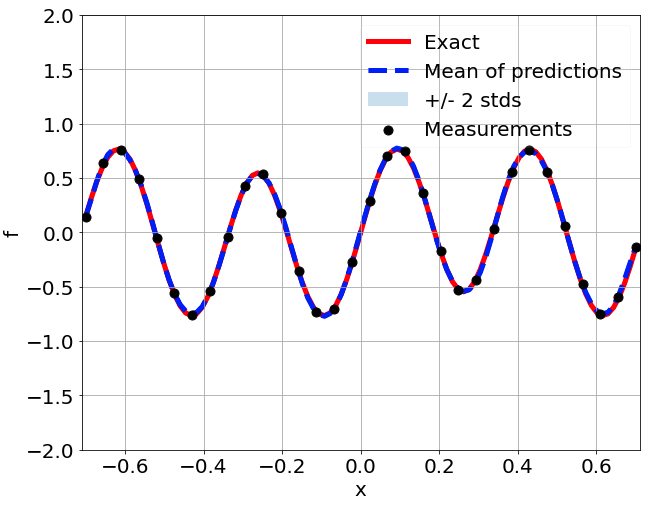
Predictions w/ \(\sigma = 0.1\) noise on measurements

Prediction \(u\) w/ raw solutions

Prediction \(f\) w/ raw solutions

Prediction \(u\) w/ \(2\sigma\) distribution

Prediction \(f\) w/ \(2\sigma\) distribution

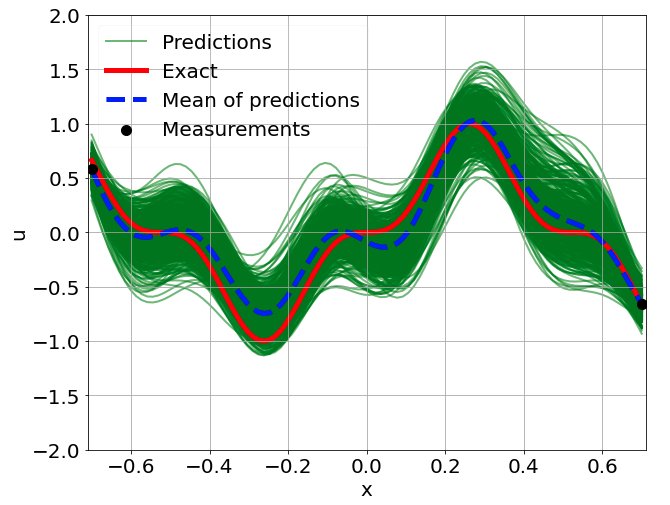
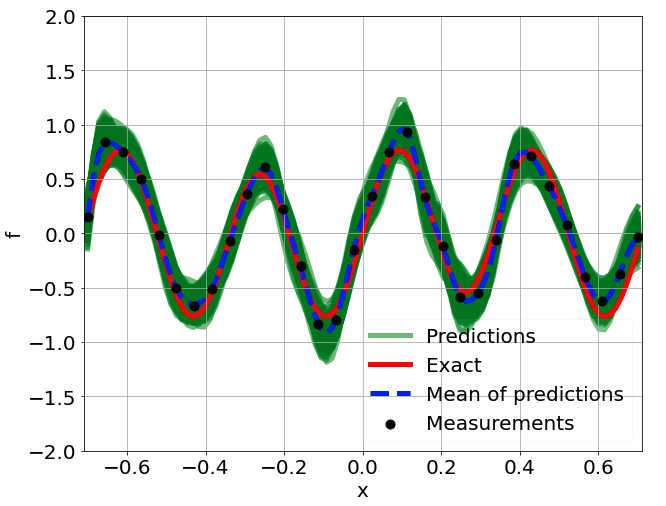
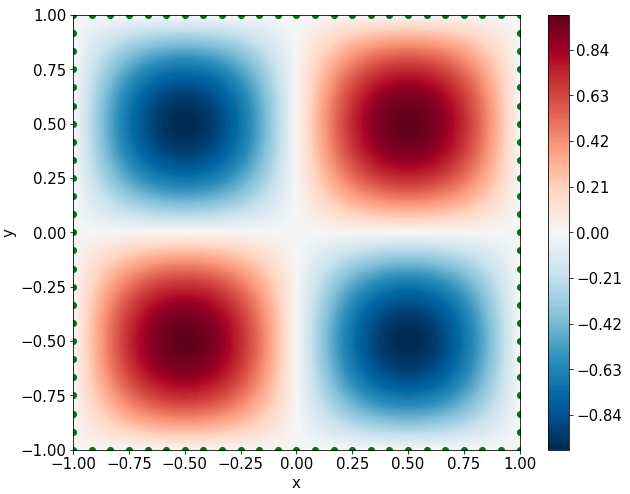
Two-dimensional nonlinear Allen-Cahn equation

\[ \begin{gathered} \lambda \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) + u\left(u^2 -1 \right) = f, \qquad x,y \in [-1, 1] \end{gathered} \] where \(\lambda = 0.01\) and \(u=\sin(\pi x)\sin(\pi y)\)

Solution \(u\)

Source \(f\) from manufactured solution

Network architecture and hyperparameters

  • 2 neural networks: \(u_{NN}\) and \(f_{NN}\)

  • 3 hidden layers with 200 neurons each

  • \(\tanh\) activation function

  • ADAM optimizer

  • \(10^{-3}\) learning rate

  • Xavier normalization

  • 50000 epochs

  • 2000 outputs

Predictions w/ \(\sigma = 0.01\) noise on measurements

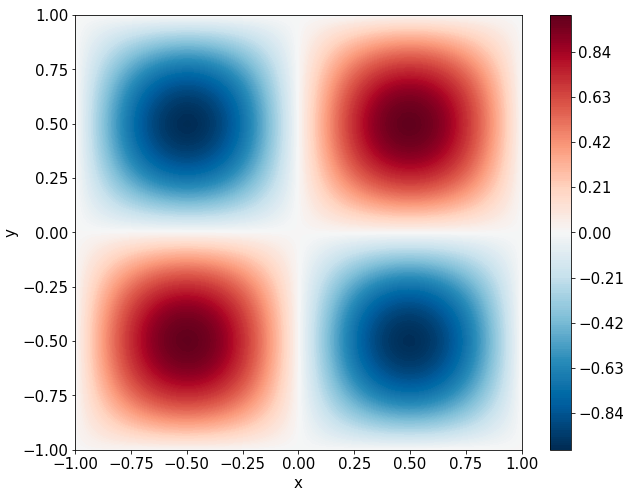
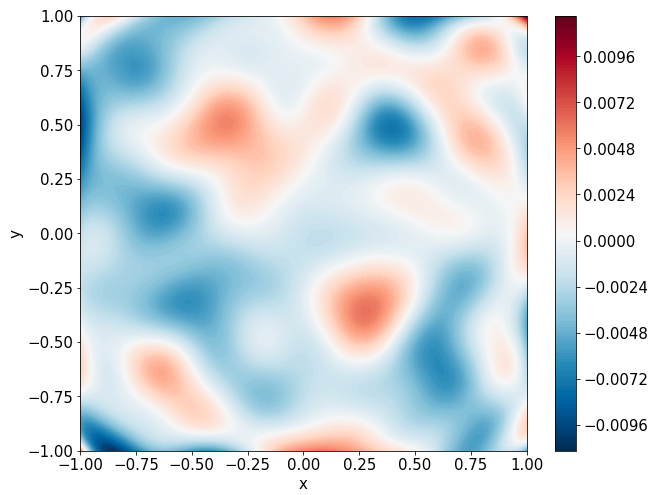
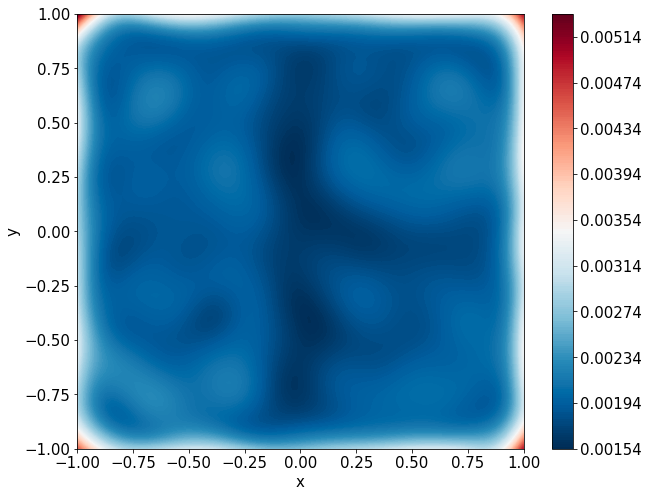
Prediction \(u\)

\(L_2\) error

Standard deviation of predictions

Bounded by 2\(\sigma\) – red = bounded, blue = not bounded

Predictions w/ \(\sigma = 0.1\) noise on measurements

Prediction \(u\)

\(L_2\) error

Standard deviation of predictions

Bounded by 2\(\sigma\) – red = bounded, blue = not bounded

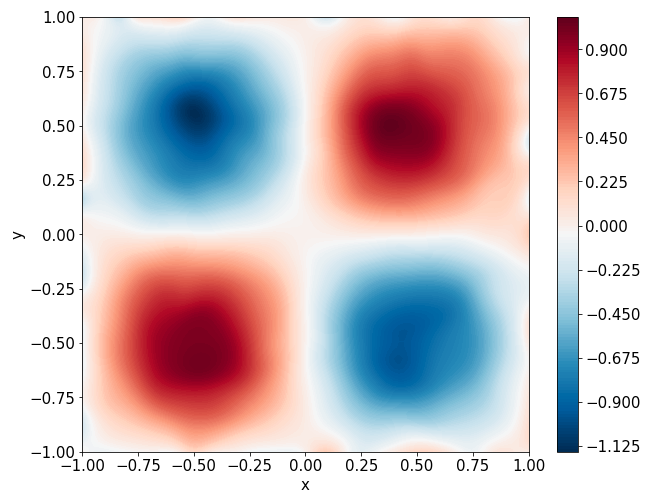
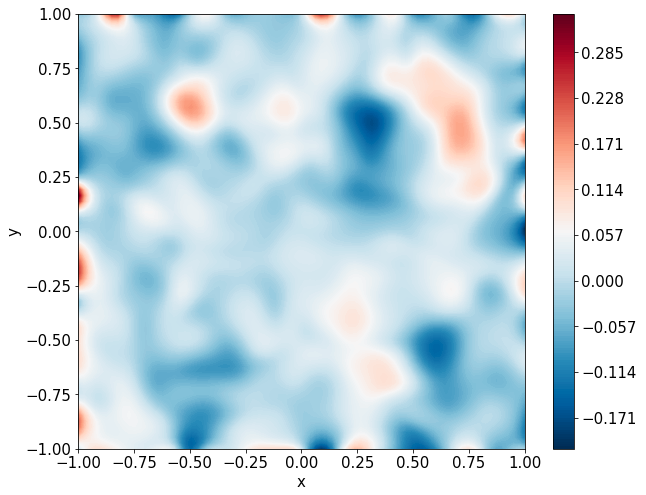
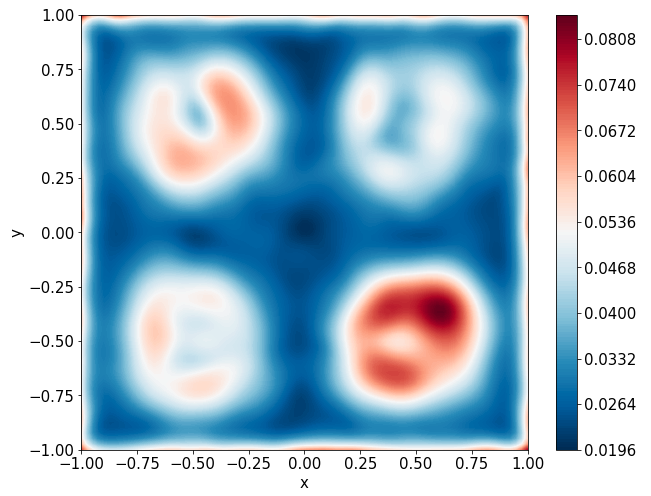
Inverse Problems

One-dimensional nonlinear Poisson equation

\[ \begin{gathered} \lambda \frac{\partial^2 u}{\partial x^2} + k \tanh(u) = f, \qquad x \in [-0.7, 0.7] \end{gathered} \] where \(\lambda = 0.01\).

\(k=[???, ???, ???, \dots, ???]\) with \(N\) entries corresponding to \(N\) outputs of the MO-PINN

Predictions

\(u\) and \(f\)

Prediction \(u\) w/ \(\sigma=0.01\) noise

Prediction \(u\) w/ \(\sigma=0.1\) noise

Prediction \(f\) w/ \(\sigma=0.01\) noise

Prediction \(f\) w/ \(\sigma=0.1\) noise

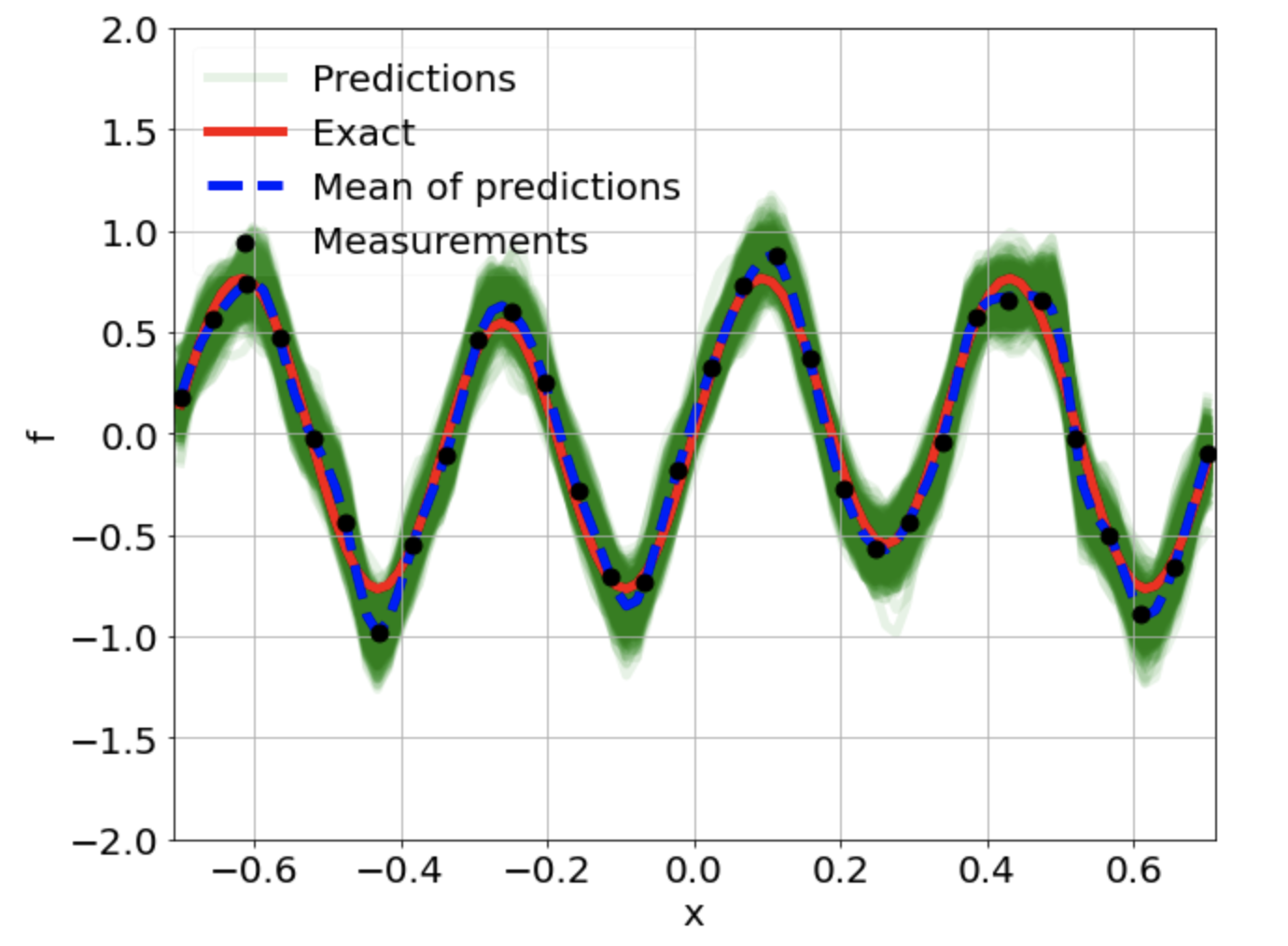
Inverse Estimates

\(k_{exact} = 0.7\)

\(\sigma=0.01\) noise, \(k_{avg} = 0.698\)

\(\sigma=0.1\) noise, \(k_{avg} = 0.678\)

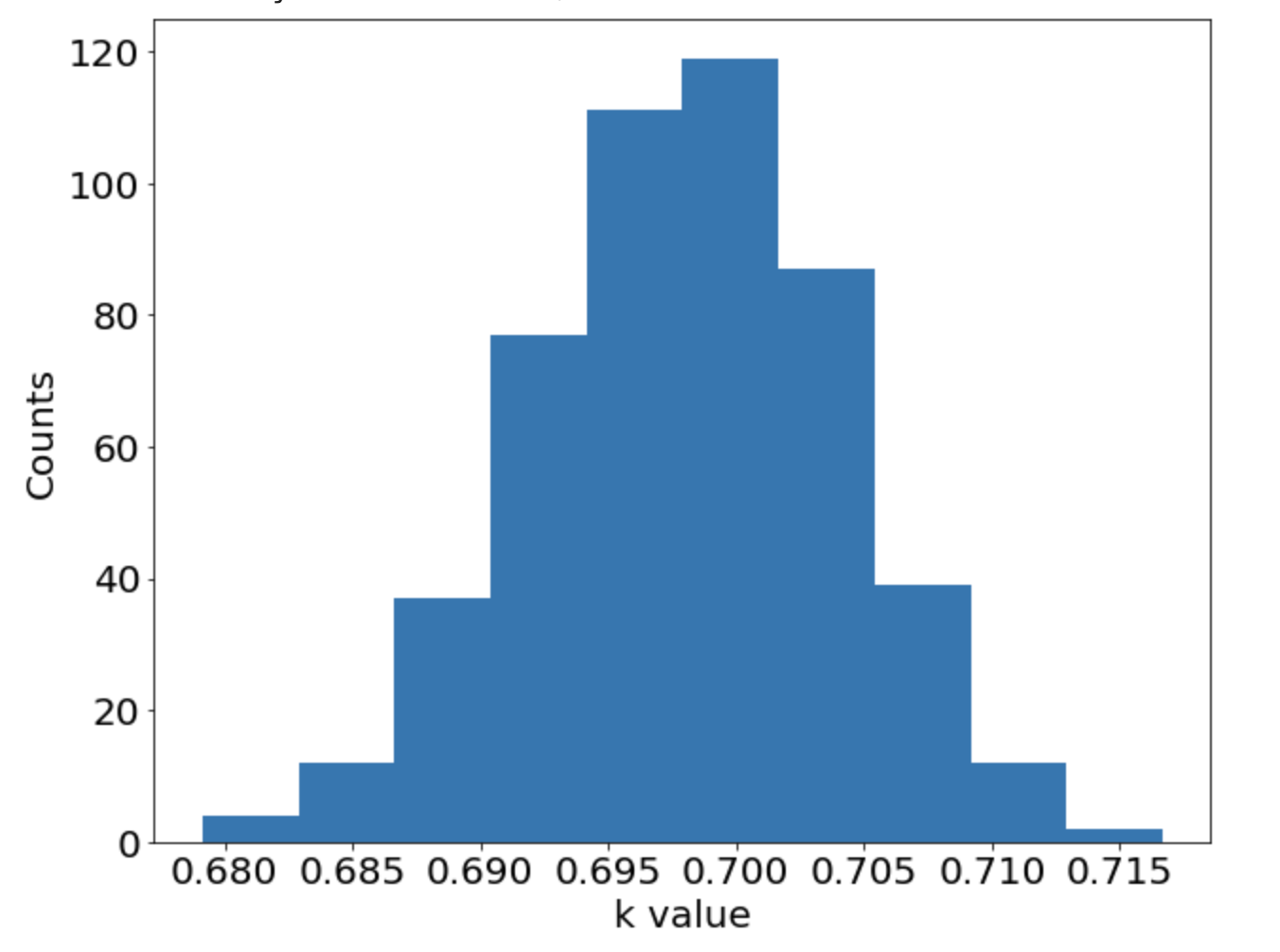
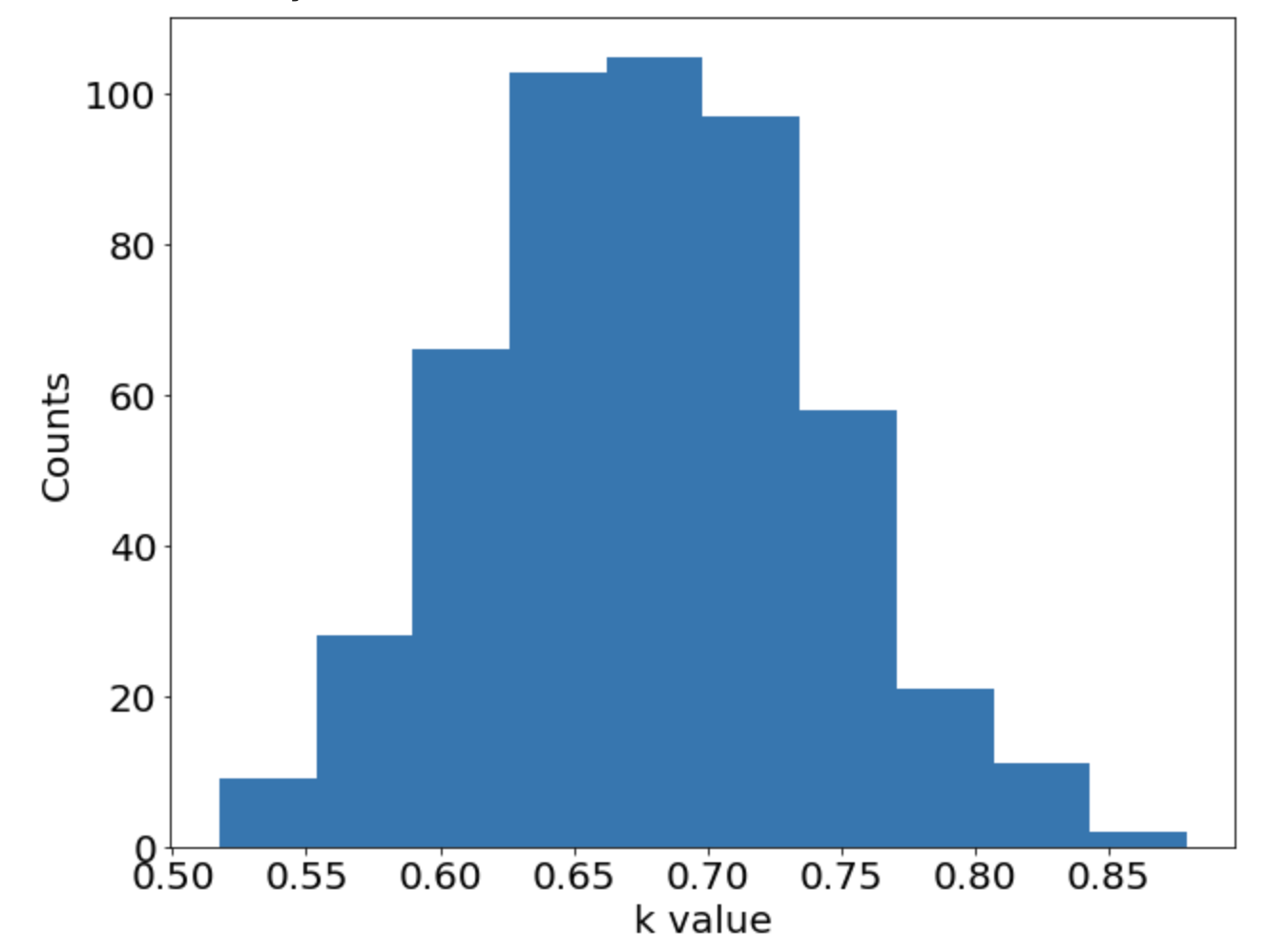
Sensitivity of \(k_{avg}\) w.r.t number of outputs

\(\sigma=0.1\) noise

10 outputs, \(k_{avg} = 0.67\)

50 outputs, \(k_{avg} = 0.684\)

100 outputs, \(k_{avg} = 0.668\)

500 outputs, \(k_{avg} = 0.673\)

Two-dimensional Allen-Cahn Equation

\[ \begin{gathered} \lambda \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) + u\left(u^2 -1 \right) = f, \qquad x,y \in [-1, 1] \end{gathered} \] where \(\lambda = 0.01\) and \(u=\sin(\pi x)\sin(\pi y)\)

\(k=[???, ???, ???, \dots, ???]\) with \(N\) entries corresponding to \(N\) outputs of the MO-PINN

Solution \(u\) and measurements

Solution \(f\) and measurements

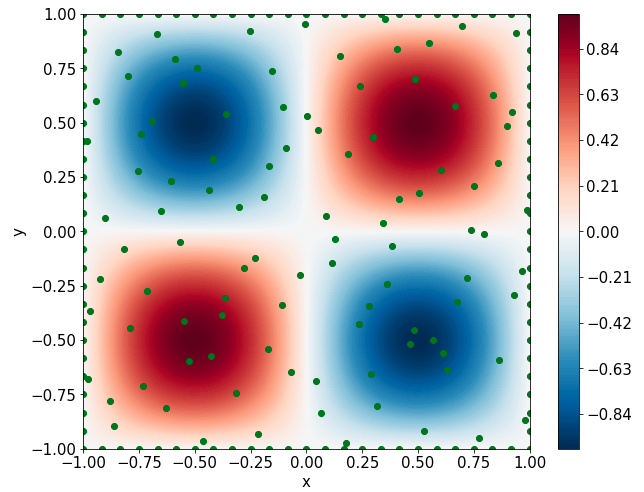
Inverse Estimates

\(k_{exact} = 1.0\)

\(\sigma=0.01\) noise, \(k_{avg} = 0.995\)

\(\sigma=0.1\) noise, \(k_{avg} = 1.02\)

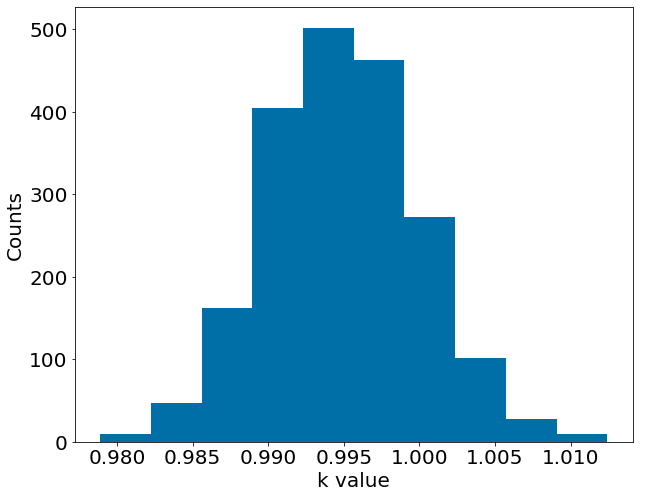
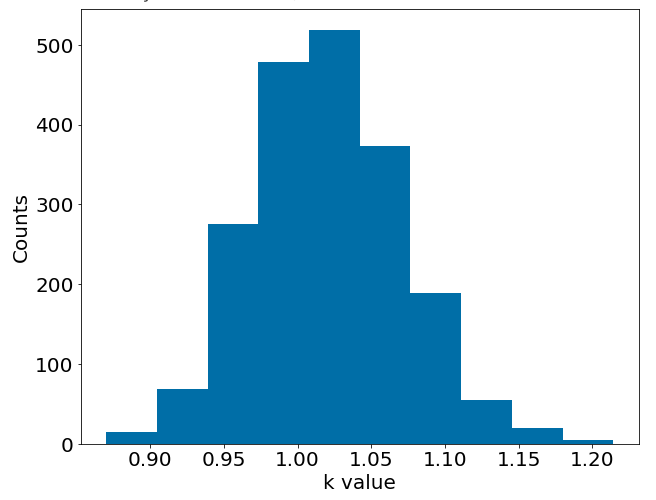
Incorporating prior statistical knowledge

Comparison to Monte Carlo FEM

One-dimensional linear Poisson equation

MO-PINN prediction of \(u\)

FEA prediction of \(u\)

MO-PINN prediction of \(f\)

FEA prediction of \(f\)

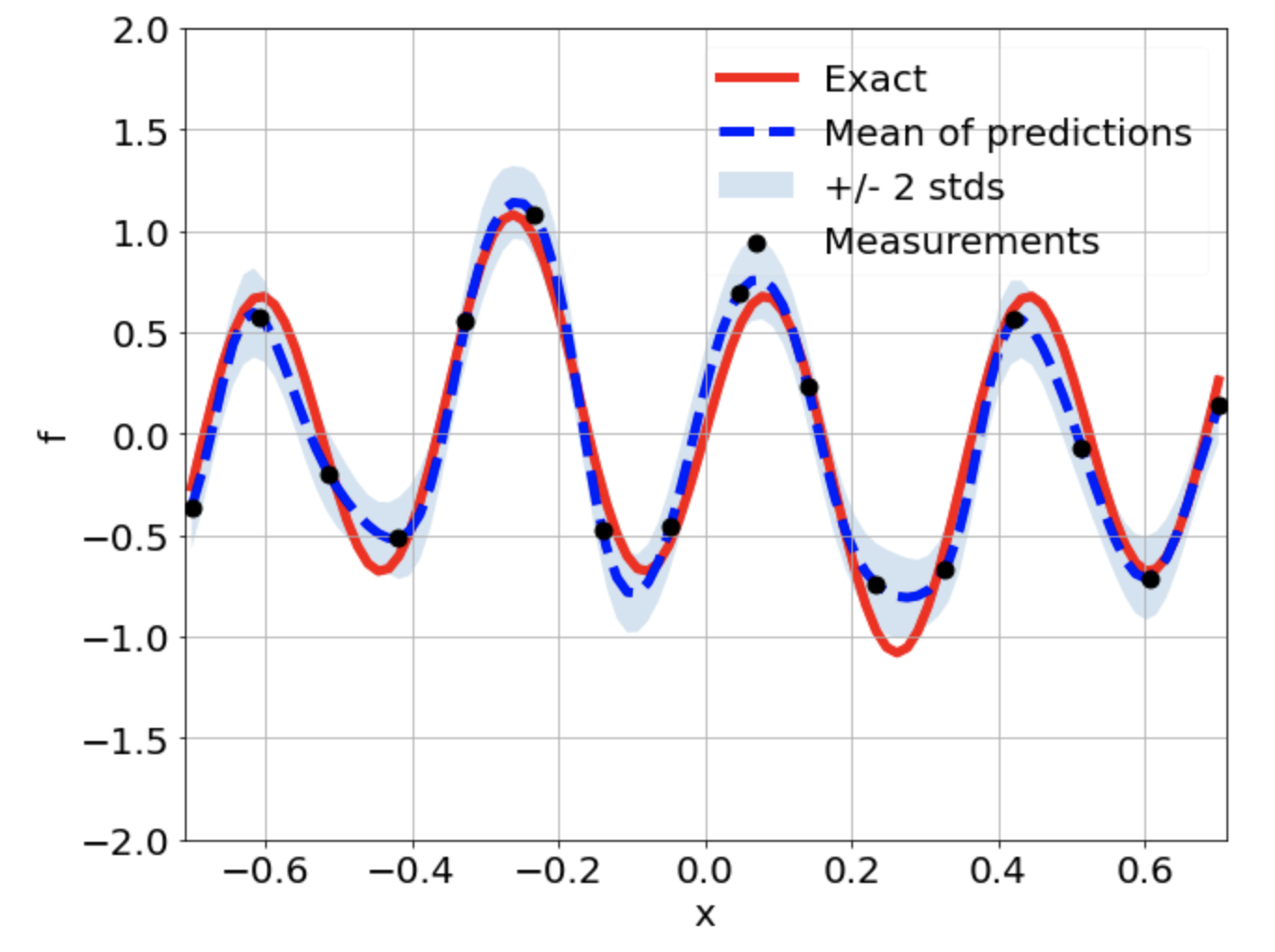
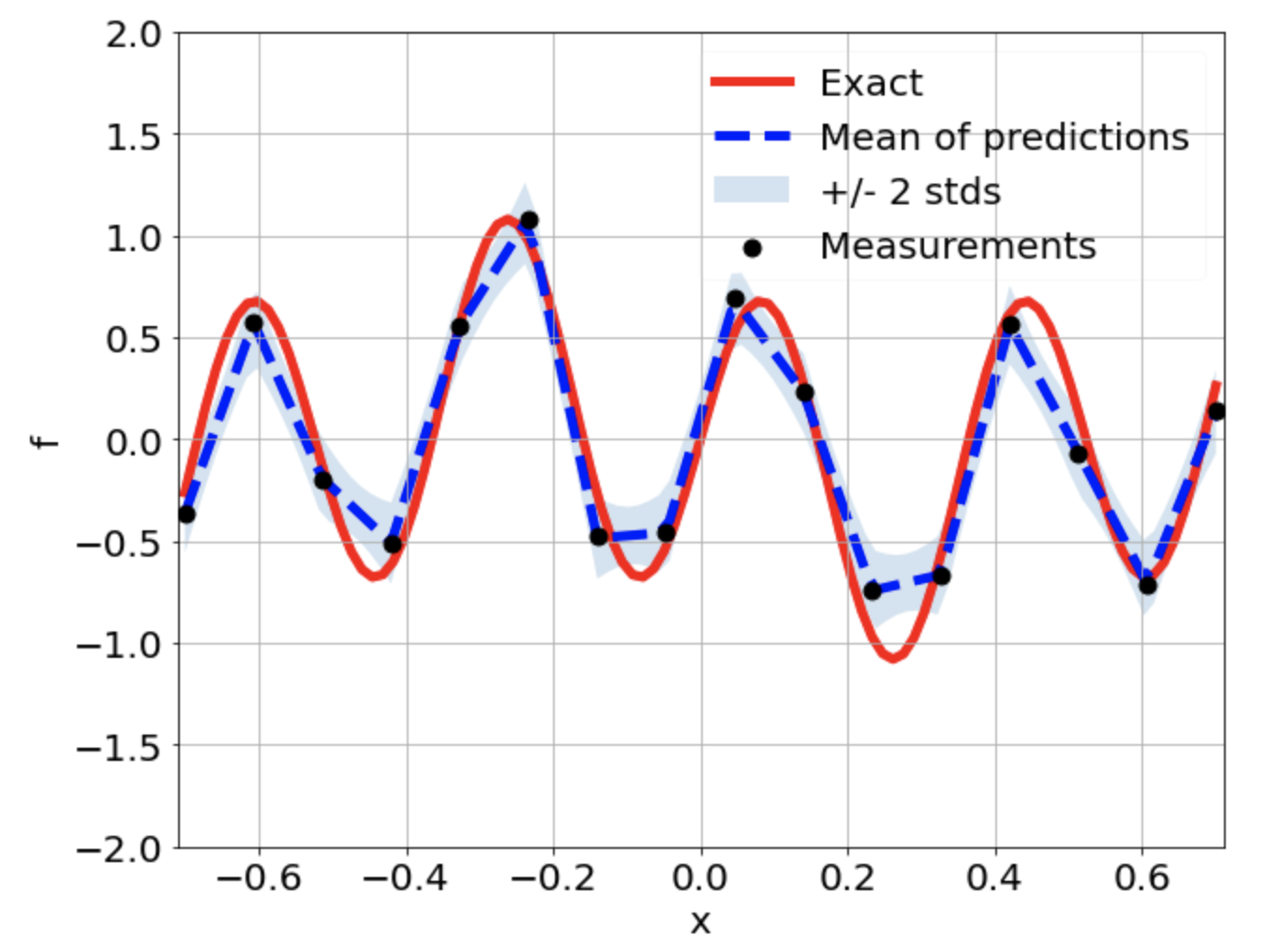
Comparison of distributions

MO-PINN vs. FEA Monte Carlo

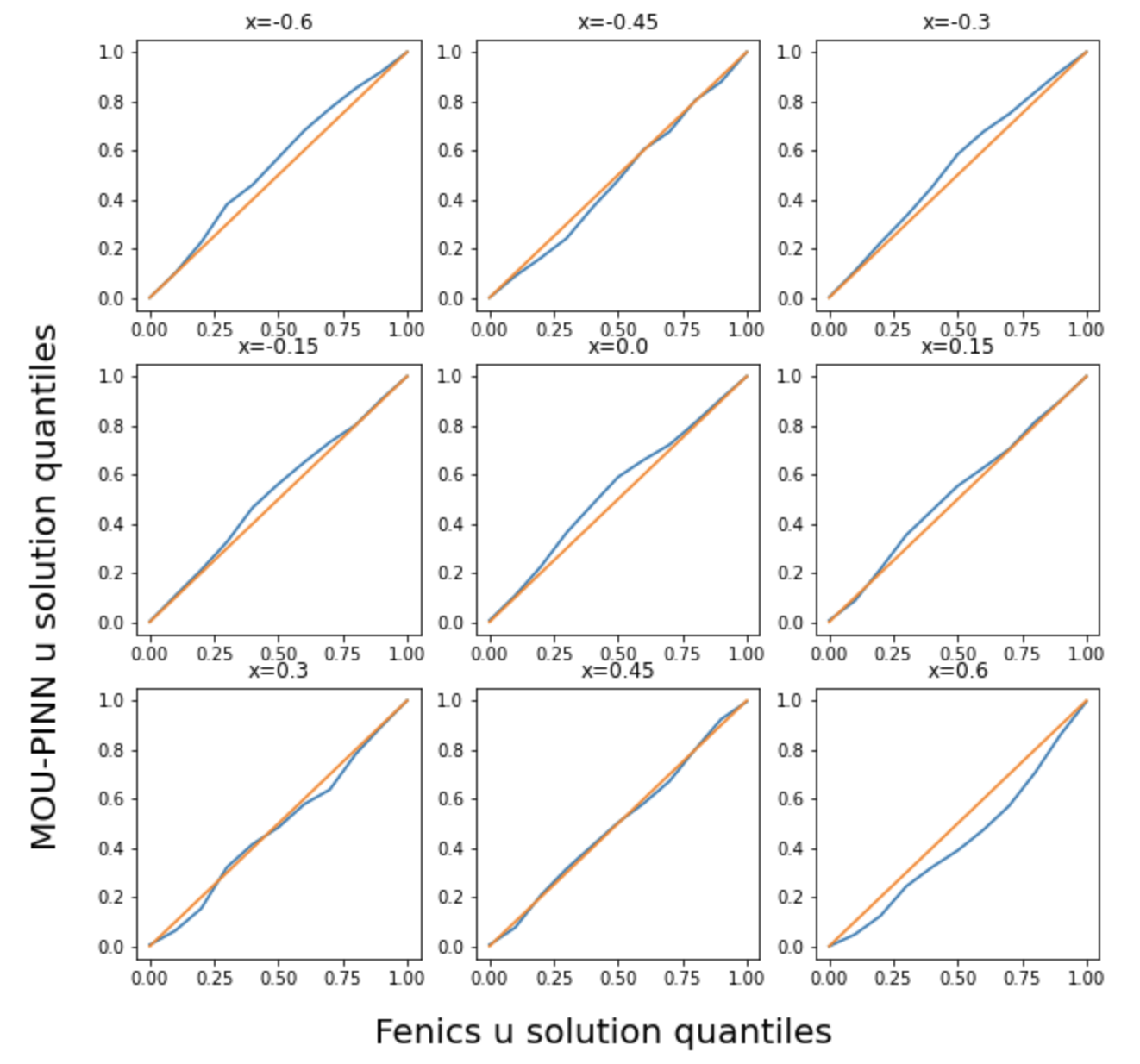
Quantile-quantile plot of \(u\) at 9 locations

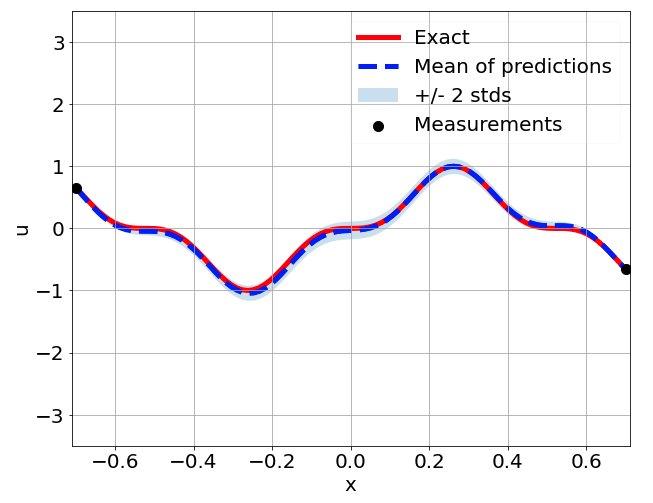
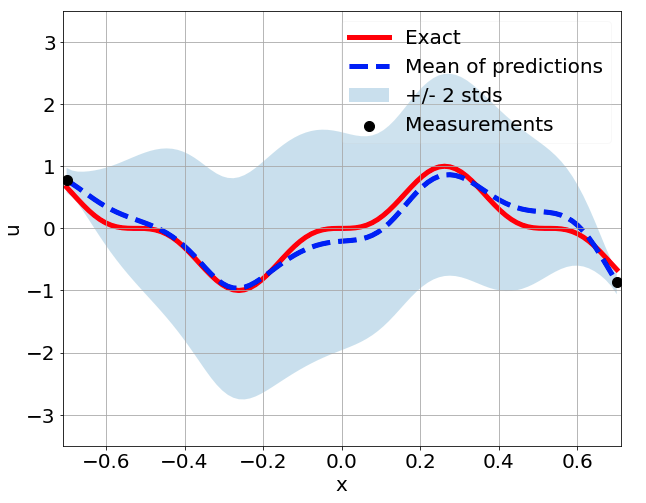
\(u\) predictions with only 5 measurements

Using mean and std to enhance learning

Only 5 measurements

5 measurements and mean

5 measurements, mean, and std

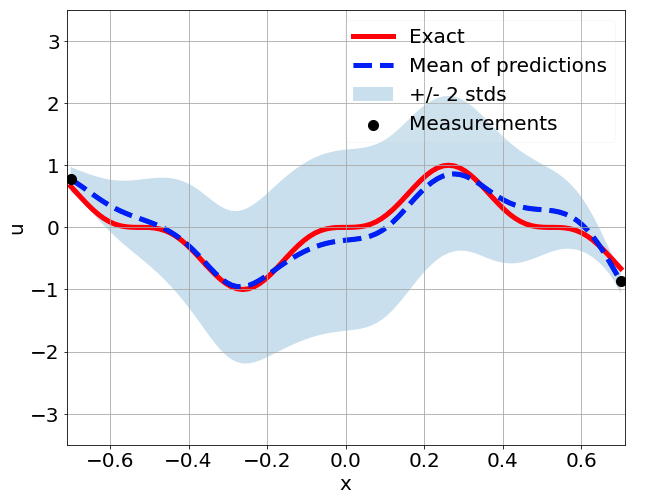
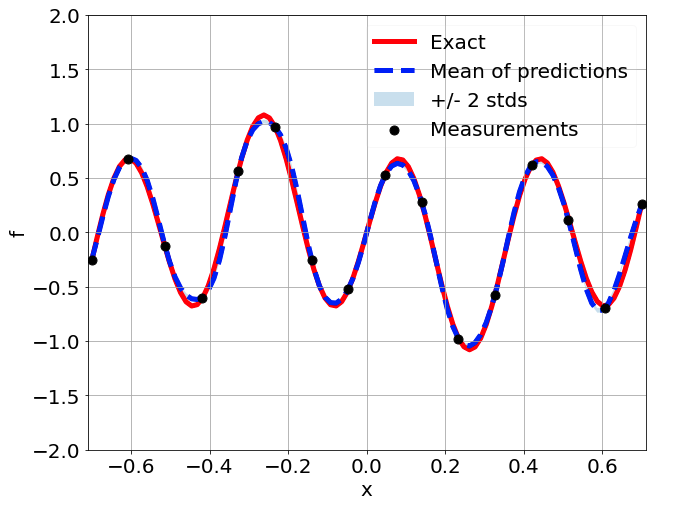
\(f\) predictions with only 5 measurements

Using mean and std to enhance learning

Only 5 measurements

5 measurements and mean

5 measurements, mean, and std

Conclusions

  • MO-PINNs appear promising for UQ
  • MO-PINNs can learn solution, source terms, and parameters simultaneously
  • MO-PINNs are faster than Monte Carlo forward solutions for the problem studied
    • Only need to train a single network

References

Jiang, Xinchao, Xin Wanga, Ziming Wena, Enying Li, and Hu Wang. 2022. “An e-PINN Assisted Practical Uncertainty Quantification for Inverse Problems.” arXiv Preprint arXiv:2209.10195.
Raissi, Maziar, Paris Perdikaris, and George E Karniadakis. 2019. “Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations.” Journal of Computational Physics 378: 686–707.
Yang, Liu, Xuhui Meng, and George Em Karniadakis. 2021. “B-PINNs: Bayesian Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Noisy Data.” Journal of Computational Physics 425: 109913.
Yang, M., and J. T. Foster. 2022. “Multi-Output Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Uncertainties.” Computer Methods in Applied Mechanics and Engineering, 115041. https://doi.org/10.1016/j.cma.2022.115041.